Cunoaște Intuit, curs, combinatorică de partiții

Rezumat: Introducere. Sarcini. Diferite statistici. Arbori și permutări de n elemente. CMN Numărul de combinații. Provocări pentru numerele de pereți despărțitori. Probleme combinatorie a teoriei informației.

Provocările pe care le considerăm acum elementele sunt împărțite în grupuri, precum și necesitatea de a găsi toate căile această secțiune. În același timp, se poate întâlni cu diferite ocazii. Uneori joacă un rol semnificativ în ordinea elementelor în grupe: de exemplu, atunci când steagurile de semnal impiegatul post pe mai multe catarge, atunci este important nu numai pe un stâlp va fi acest lucru sau că pavilion, dar, de asemenea, ordinea în care sunt agățate steagurile. În alte cazuri, ordinea elementelor în grupe de nici o importanță. Când jucătorul selectează zarurile piesele de domino din gramada, nu contează în ce ordine vor veni, ci doar rezultatul final este important.

Sarcini diferite și dacă rolul jucat de ordinea grupurilor propriu-zise. Într-un joc de domino jucători ședinței într-o anumită ordine, și este important nu numai cum să împartă os, dar, de asemenea, care a primit nici un os. Dacă așezați fotografii ale acelorași plicuri pentru a le distribui, la fel ca fotografiile partajate în plicuri, dar ordinea plicurilor ei înșiși complet irelevante.

Joacă un rol și că distincția între elementele ei sau nu, precum și distincția între dacă un grup, care sunt împărțite în elemente. În cele din urmă, în unele probleme, unele grupuri pot fi goale, adică nu conțin nici un element, și alte astfel de grupuri nu sunt permise. În conformitate cu toate cele de mai sus, există un număr de diferite probleme combinatoriale pe partiție.

Formularea generală a acestor sarcini:

Problema 1. Dispunerea sertare

Având în vedere diferite articole și cutii. Este necesar să se pună în prima cutie de articole în al doilea - elemente. în cazul în care lucrurile lea - cât de multe moduri în care puteți face o astfel de distribuție?

Numărul de aspecte diferite pe aceleași casete

Această formulă poate fi obținută prin rezolvarea următoarelor la prima vedere, destul de diferit problema:

Problema 2. Permutări cu repetiție.

Există diferite tipuri de obiecte. Cât de multe diferite permutări pot fi făcute de obiecte de primul tip, al doilea tip de obiecte. lea tip de obiecte? Numărul de obiecte din fiecare permutare de îngrijire. Prin urmare, în cazul în care toate elementele sunt diferite, numărul de permutări ar fi egale. Dar, din cauza faptului că unele dintre elementele sunt aceleași, veți obține un număr mai mic de permutări. De fapt, să luăm, de exemplu, permutarea

în care primele scrise toate elementele primului tip, atunci toate elementele de al doilea tip. În cele din urmă, toate elementele de tip lea. Elementele din primul tip pot fi interschimbate unii cu alții! moduri. Dar, întrucât toate aceste elemente sunt aceleași, astfel de rearanjamente nu se schimba nimic. În mod similar, nu se schimbă nimic! permutări ale elementelor de al doilea tip. ! Elemente de tip permutare -lea.

Permutare a elementelor primului tip, al doilea tip și așa mai departe se poate face independent. Prin urmare, elementele de transpunere 5.1. pot fi interschimbate unii cu alții! moduri, astfel încât să rămână neschimbată. Același lucru este valabil și pentru orice alt aranjament al elementelor. Prin urmare, setul de toate! permutări se destrame, constând! identică fiecare permutare. Prin urmare, numărul diferitelor permutări cu repetiții, care pot fi trase din elementele de date, precum și

5.2 Cu ajutorul formulei, putem răspunde la întrebarea: cât de multe permutări pot fi făcute din literele cuvântului „Mississippi“? Aici avem o litera „m“, cele patru litere „și“ trei litere „c“ și o literă „n“, și un total de 9 litere. Deci, în conformitate cu formula 5.2 numărul de permutări de același

Pentru a stabili legătura dintre aceste probleme, vom enumera toate locurile care pot lua lucrurile noastre. Fiecare permutare corespunde distribuției locurilor în clasa camerei. Prima clasă include numărul de locuri, care au fost obiecte de primul tip, al doilea - numărul de locuri de obiecte de al doilea tip, și așa mai departe. Aceasta stabilește o corespondență între permutările cu repetiții și dispunerea de locații camere de „“ Este clar că formula de rezolvare a problemelor au fost aceleași.

În obiectivele de mai sus, nu se ia în considerare modul în care există elemente ale fiecărei părți. În unele aplicații, ar trebui să fie luate în considerare această procedură.

Problema 3. Steaguri catarge.

Există o varietate de steaguri semnal și stâlpi, pe care le atârnă. valoarea semnalului depinde de ordinea în care sunt agățate steagurile. Cât de multe moduri se poate închide steaguri dacă ar trebui să fie utilizate toate steagurile, dar unele dintre catargelor poate fi gol?

Fiecare metodă de agățat steaguri poate fi realizată în două etape. La prima etapă vom face schimb de date în orice mod posibil steaguri. Se poate face! moduri. Atunci una dintre modalitățile de distribuire a catargele steaguri identice (număr de moduri). Lăsați această metodă constă în faptul că primul pilon este necesar să stea steagurile de pe al doilea - steaguri. pe steaguri lea, care apoi ia primul steag al secvenței și atârnă în ordinea primirii primului pilon; Următoarele steaguri sunt agățate pe al doilea pilon, etc. Este clar că, folosind toate permutări steagurile și toate modurile de distribuire a acelorași steaguri pe catarge, vom găsi toate căile de a rezolva această problemă. Conform regulii de lucrări constatăm că numărul de moduri de steaguri agățat oricum

În general, în cazul în care există o varietate de lucruri, numărul de moduri de a distribui aceste lucruri în cutii diferite, oricum

alte statistici

Problema dispunerea obiectelor de pe cutii sunt foarte importante în fizica statistică. Acest studii științifice modul în care distribuite pe proprietățile fizice ale particulei; de exemplu, pe care o parte din moleculele unui anumit gaz la o temperatură dată are o anumită viteză. În acest caz, setul de toate stările posibile este distribuit la un număr mare de celule mici (state de fază), astfel încât fiecare dintre particule se încadrează într-una din celule.

Problema a ceea ce statisticile sunt supuse anumitor particule, depinde de tipul de particule. În fizica statistică clasică, creată de particule Maxwell și Boltzmann sunt considerate distinse unul de celălalt. Astfel de statistici sunt supuse, de exemplu, moleculele de gaz. Este cunoscut faptul că diferite particule pot fi împărțite între celulele de moduri. În cazul în care toate aceste metode pentru o anumită energie au o probabilitate egală. atunci vorbim despre statisticile Maxwell-Boltzmann.

Sa dovedit că aceste statistici nu se supun toate obiectele fizice. Fotonii, nucleele atomice și atomi care conțin un număr par de particule elementare se supun diferite statistici dezvoltate de Einstein și Bose Indian om de știință. In particule Bose-Einstein sunt considerate imposibil de distins unul față de celălalt. Prin urmare, este important acest lucru este cât de multe dintre particule se încadrează într-o anumită celulă, și nu exact ceea ce particulele de ajuns acolo.

Cu toate acestea, pentru multe dintre particule, cum ar fi electroni, protoni și neutroni nu sunt adecvate, iar statisticile Bose-Einstein. Pentru ei, în fiecare celulă poate fi localizată, nu mai mult de o particulă, distribuția diferită a satisface condițiile specificate, au o probabilitate egală. În acest caz, acesta poate fi de diferite distribuții. Această statistică se numește Fermi statistici Dirac.

Arbori și permutări de n elemente

Cu ajutorul pădurii poate fi reprezentată de o permutare a elementelor setului (un set de definim: set - este o colecție neordonată diferitelor obiecte sau structuri de date utilizate pentru a reprezenta setul.). Sa calcula cât de mult puteți obține permutări. Pentru o astfel de lemn este prezentată în Fig. 5.1.

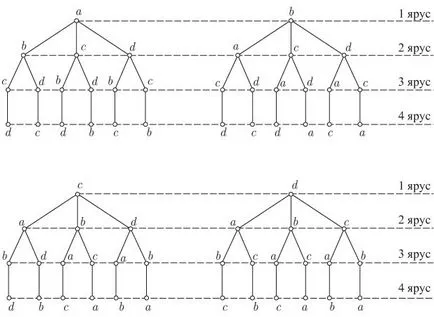
Fig. 5.1. Diferite permutări ale acestui model sunt citite din vârful rădăcină corespunzătoare lemnului agățat. Nivelul arată numărul de locul în care se află elementul. Numărul de noduri pandantiv de pădure egal cu numărul de permutări