Compass-și-dreptar de construcții - este

Compass-and-dreptar constructii

Construcții cu rigla și compasul - secțiune a geometriei euclidiene. cunoscut inca din cele mai vechi timpuri. Sarcinile de a construi o busolă și conducător sunt considerate instrumente ideale, în special:

• Linia nu are divizii și are o față de lungime infinită, dar numai unul.
• Compasul poate fi arbitrar soluție mare sau mică arbitrar (adică, se poate trage o rază de cerc arbitrar).

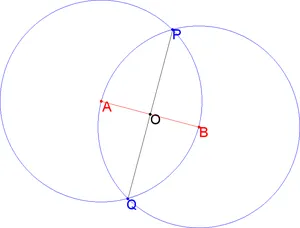
Divizarea în jumătate de lungime

Provocarea pentru împărțire în două. Cu ajutorul unui conducător și busolă împarte segmentul AB în două părți egale. O soluție este prezentată mai jos:

• Compase dețin un cerc centrat la punctele A și B raza AB.
• Găsiți punctele de intersecție P și Q două cercuri construite (arce).
• Prin efectuarea segment de linie sau o linie care trece prin punctele P și Q.
• Vom găsi AB punctul de mijloc necesar - punctul de intersecție al AB și PQ.

Definiția formală

Sarcinile de construcție sunt considerate set de toate punctele în plan, setul plan de toate liniile și setul de toate cercurile planului pe care sunt permise următoarele operații:

1. Selectați un punct din setul tuturor punctelor:
   1. un punct arbitrar
   2. punct arbitrar de pe linia de date
   3. punct arbitrar de pe circumferință predeterminată
   4. punctul de intersecție a două linii de date
   5. punctul de intersecție / touch linie dată și un anumit cerc
   6. punctul de intersecție / contact a două cercuri date
2. „Cu ajutorul unui conducător“ pentru a aloca direct din setul de toate liniile:
   1. linie arbitrară
   2. o linie arbitrară care trece printr-un anumit punct
   3. o linie dreaptă care trece prin cele două puncte specificate
3. „Cu ajutorul unui compas“ evidenția circumferința din multitudinea de cercuri:
   1. cerc arbitrar
   2. cerc arbitrar centrat la un punct predeterminat
   3. cerc arbitrar cu o rază egală cu distanța dintre două puncte
   4. cerc cu centrul la un anumit punct și cu o rază egală cu distanța dintre două puncte

În ceea ce privește problema este dată de un set de puncte. Necesar de un număr finit de operații ale numărului de operații permise sunt enumerate mai sus pentru a construi un alt set de puncte situate la un raport predeterminat cu setul inițial.

Soluție pentru construirea conține trei părți esențiale:

1. Descrierea metodei de construire a unui set dat.
2. Dovada că set construit așa cum este descris, este într-adevăr, într-un raport predeterminat cu setul inițial. De obicei, construcția de probă este produs ca o dovadă normală a teoremei, bazată pe axiome și alte teoreme s-au dovedit.
3. Analiza metodei descrise pentru construirea aplicabilitatea sa la diferite exemple de realizare, condițiile inițiale, și, de asemenea, pentru unicitatea sau soluțiile descrise pot obține non-unicitate.

problemă cunoscută

• Problema construirii Apolonius cerc ating trei circumferințe predeterminate. Dacă nici unul din cercul specificat nu se află în interiorul celuilalt, această problemă are 8 soluții în mod substanțial diferite.
• Sarcina de a construi Brahmagupta patrulater înscris pe cele patru laturi ale sale.

Construirea poligoane regulate

Construirea unui pentagon regulat

geometri antice fost cunoscute metode de construire n -gons regulate pentru ,, și.

In 1796, Gauss a demonstrat posibilitatea construirii unei n corecte -gons atunci când, în cazul în care - distincte amorse Farm. În 1836, Pierre Wantzel a dovedit că alte poligoane regulate care pot fi construite cu rigla și compasul, nu există.

Probleme nerezolvate

Următoarele trei probleme cu privire la construcție au fost puse în antichitate:

• trisecțiunea unghiului - unghi arbitrar împărțit în trei părți egale.
• Dublare cub - construi o margine cub de două ori mai mult volum decât cubul
• Cvadratura cercului - de a construi un pătrat egal în zona acestui cerc.

Abia în secolul al XIX-lea, sa dovedit că toate cele trei probleme sunt de nerezolvat, folosind numai rigla și compasul. Pun la îndoială posibilitatea de a construi un sistem complet rezolvată prin metode algebrice bazate pe teoria lui Galois.

• Un alt celebru nerezolvat folosind busola si rigla sarcina - pentru a construi un triunghi de trei Bisectoarele o lungime predeterminată. [1] Mai mult decât atât, această problemă rămâne nerezolvată chiar și în prezența trisektora. [2]

Este posibil și imposibil de a construi

Toate construcțiile nu sunt nimic altceva decât deciziile orice ecuație. în care coeficienții ecuației asociate cu lungimi predeterminate ale segmentelor. Prin urmare, este convenabil să vorbim despre construcția - soluția grafică a ecuației de un anumit tip. Ca parte a cerințelor de mai sus, următorul construct:

Cu alte cuvinte, este posibil să se construiască un număr egal cu expresii aritmetice, folosind rădăcina pătrată a numerelor de intrare (lungimi segment). De exemplu,

• În cazul în care numai un segment de lungime, este imposibil să ne imaginăm în această formă (prin urmare, imposibilitatea cubului de dublare).
• Posibilitatea de a construi o regularitate de 17-gon rezultă din cosinusul unghiului:

Variații și generalizări

• Construcții cu o singură busolă. Prin teorema lui Mohr - Mascheroni folosind o busolă, puteți construi orice forma pe care o puteți construi o busolă și dreptar. Atunci când acest lucru este considerat a fi construit direct, în cazul în care două puncte sunt stabilite pe ea.
• Construit folosind aceeași linie. Este ușor de observat că singurul invariantul proiectivă de construcție poate fi realizată cu o singură linie. În special, este imposibil chiar să împartă segmentul în două părți egale, sau pentru a găsi centrul cercului desenat. Dar prezența avionului în avans efectuate de un cerc cu un centru marcat cu un conducător poate face aceeași construcție ca și conducător și busolă (Poncelet teorema -. Steiner (engleza)), 1833. Dacă linia are două crestături, construcția cu ajutorul ei construcții echivalente cu rigla și compasul (pas important în a dovedi că Napoleon a făcut).
• Construit folosind instrumentele cu handicap. Problemele de acest tip de instrumente (spre deosebire de formularea clasică a problemei) sunt considerate nu este ideal, dar limitate: o linie dreaptă prin cele două puncte cu un conducător poate fi efectuată numai cu condiția ca distanța dintre aceste puncte nu depășește o anumită valoare; cercuri de rază conduse cu un șubler poate fi limitată la partea de sus, de jos sau ambele partea de sus și de jos.
• De a construi cu un origami plat. cm. Hudzita reguli

fapte interesante

• Modelul de pavilion este descris ca Iran construcție cu rigla și compasul [3].

• aplicație dinamică Geometrie vă permite să construiască cu rigla și compasul pe un computer.

notițe

literatură