salturi de etanșare

Partea din stânga a secțiunii de pe partea dreaptă a N.  pe P 1.

Cu o creștere nelimitată a presiunii de șoc (P ) creșterea densității are o limită în șoc

Aer (5.13)

5.4. unda de șoc Oblic

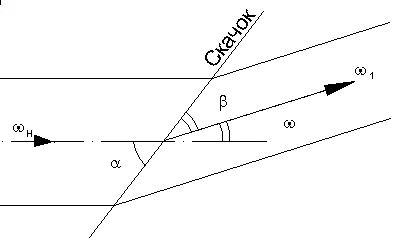
Oblică unda de șoc a frontului de undă de șoc este înclinată față de direcția de curgere. Apare cand saltul frontal traversat, debitul de gaz trebuie să schimbe direcția, de exemplu, în corpul supersonic pană de curgere a gazului.

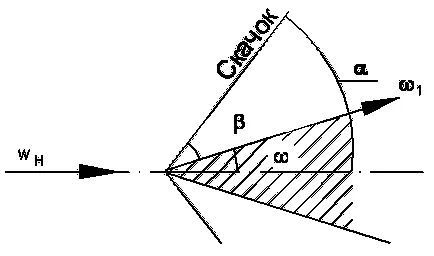
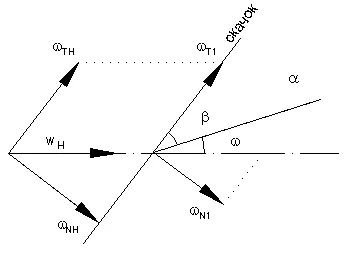
Descompune vectorii de viteza pentru a sari  H și după salt  1 în componente paralele și marginea frontală normală a undei de șoc (salt). În acest caz, componenta tangențială rămâne constantă  t = const. o componentă normală scade  NH>  N1.

inhibarea parțială 5.5.Temperatury

Șocul oblic curgerii ecuației izolate entalpie

Triunghiul de viteze

Derivarea conceptul de inhibare parțială a temperaturii, realizând sub temperatură care nu va avea debitul la frânare completă, dar numai la maturitate normală a componentelor vitezei față de șoc

parametrii de curgere în stare de șoc 5.6.Opredelenie oblic. Cinematica șoc oblice

Determinarea parametrilor de curgere în șoc oblică

Dacă luăm în considerare ecuația de stat sub formă de

se poate demonstra că rasele de etanșare oblice descrise de aceleași ecuațiile ca rasele drepte, cu singura diferență că, în primul caz, în loc de rata integrală sunt normale la partea din față a componentei șoc, dar în loc de inhibare completă a temperaturii T 0 -  T temperatura de stagnare parțială .

aici - viteză critică parțială, care corespunde unei temperaturi de inhibare parțială a T .

Cinematica șoc oblice

și relația dintre viteza critică completă și parțială determinată de ecuația:

Revenind la raportul de viteză

5.7. rezistenta la unda de șoc oblice. Intensitatea șocului oblic. Unghiul de deviere în șoc oblic. (*)

rezistenta la unda de șoc oblice

Modificări ale presiunii totale și statice în șocul oblic respectiv este definit de ecuații pentru un salt directă, dacă în loc  H insert dimensiune  NH.

Intensitatea șocului oblic. Unghiul de deviere în șoc oblic.

În cazul în care asociază aceste modificări cu viteza absolută a fluxului de incidente, obținem următoarea ecuație.

Dacă afișați aceste relații în funcție de numărul de M:

care arată că, pentru aceeași viteză de curgere (M H = const) rasele oblice întotdeauna mai slabă decât directă și intensitatea acestuia variază în funcție de unghiul de înclinare a frontului de șoc pe direcția fluxului liber.

Ecuația privind raportul dintre numărul M și unghiul de înclinare a șocului

Cunoscând raportul dintre avioane, este posibil să se calculeze w unghiului, care a deviat de curgere în șoc:

luând în considerare ecuația de continuitate