Metoda de iterații simple,
Metoda este iterații simple în calculul punctului nou x pe punctul vechi.
Iterare continuă până când gruparea e precizie soluția dorită.
[Edit] algoritm de decizie
Intrare: A, b, ε.
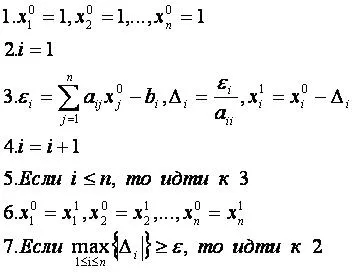
Ieșire: x.
Pentru soluții prin iteratii simple de ecuații liniare Ax = sistem b (unde A - nxn matrice pătrată a coeficienților și b - vector membri liberi ai sistemului), găsiți mai întâi sistemul principal determinant Δ.
Metoda de iteratii simple, se aplică (adică metoda convergent), dacă este determinant principal al sistemului Δ ≠ 0 și condițiile uneia dintre cele două cazuri:
1), atunci când cel puțin una dintre normele matricei B = E-A este mai mic de 1:
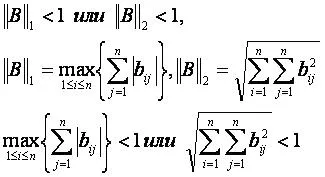
2) când toate autovalorile matricei B = E-un modul mai mic de 1.
Pentru a verifica condițiile doilea caz, este necesar să se determine valoarea λ = max1 |, | λ2 |, ..., | λn |>. în cazul în care λ1, λ2, ..., λn - autovalorile B. și verificați starea X<1 .
De obicei, matricea B = E-A satisface condițiile de mai sus, atunci când diagonala principală a matricei A sunt elementele dominante Aii;
Aii element dominant este elementul care satisface inegalitatea: