Matricea algebra - matrice transpusă

rânduri, respectiv coloane dă așa-numita matrice transpusa de dimensiune n × m:

În special, pentru strokitransponirovannoy vector-matrice este un vector coloană

Principalele proprietăți ale matricei transpuse:
1) matricea transpusă de două ori coincide cu originalul:

2) suma matricei transpuse matricelor este egală cu suma matricei transpuse de termeni, adică,

3) transpoziția produsului matrice matricelor este produsul factorilor matrice transpuse, luate în ordine inversă:

Pentru o matrice pătratică are egalitate evidentă:

Dacă matricea coincide cu transpusa ei

aceasta se numește simetrică. Din această din urmă ecuație rezultă că matricea simetrică este pătrată și elementele sale sunt simetrice diagonalei principale sunt egale:
Este evident că produsul este o matrice simetrică folosind ca proprietate de 3, obținem:

EXEMPLU EXEMPLU. Dată fiind matricea A și transpusa matricei:

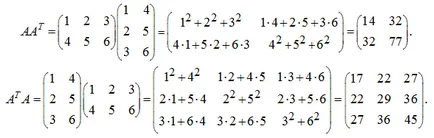
Așa cum s-ar putea fi de așteptat, a primit matrici simetrice.