Graficul funcției pătratice cu modulul "
Lecția Subiect: „Graficul unei funcții pătratice cu modulul“
Beneficiu funcția unică
(două lecții în clasă cu studiul aprofundat de matematică)
Didactic: pentru a forma capacitatea elevilor de a efectua funcții pătratice grafice. care conține module.
Metodologie: punerea în aplicare a abordării centrată pe student de învățare care asigură auto-dezvoltare a studentului individuale prin activități independente și de grup cognitive, iar vzaimoanaliz introspecție, vzaimootsenku și auto-realizare a caracteristicilor sale.
b) să dezvolte creativitatea, ingeniozitatea, elevii avizați;
c) de a dezvolta cultura vorbirii.
Educaționale: pentru a aduce un sentiment de comunitate, responsabilitate, auto-control; genera interes în studiul matematicii.
Tipul de lecție: un beneficiu lecție.PROCEDURĂ
Organizarea și începutul lecției:
Studenții au ocupat locurile, a pregătit un caiet și instrumente.
Posta subiecte, obiective și sarcini ale lecției:
Astăzi avem o funcție de „beneficiu“.
-Cine, băieți, știu ce este un „beneficiu“?
actor sau de performanță a unui actor. Primul beneficiu a avut loc în
Franța în 1735.
-Crezi că asta am sunat lecția „Benefis o funcție“?
-Astăzi, întreaga clasă va fi dedicată diagrame identice
Funcția y =? ? care conține module.
Context privind pregătirea lecție: pregătirea acestei lecții
clasa a fost împărțit anterior în grupuri.
Fiecare grup a primit funcția. care trebuia să programeze
construi o casă. Elevii au fost rugați să prezinte o lecție
construirea acestor grafice de funcții și să explice construcția lor.
III. Actualizarea susținerii cunoștințelor studenților:
Dă definiția unei funcții pătratică.
Funcția este definită prin formula
Coordonatele sunt vârful parabolei:
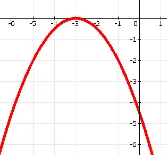
4. În ceea ce este ilustrat graficul
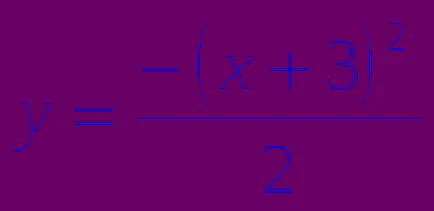
a)

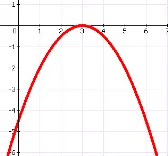
5. La ce ilustrează graficul
Jocul „plotter“
Conform graficului funcției determina semnul a, b, c, d
IV. Construirea grafice funktsіy:
Alcatuim grafice de funcții și să descrie un algoritm pentru construirea
Fiecare grup este pe ordinea de un grafic al funcției
Acesta descrie construirea unui algoritm.
y = x2 + 6│h│ 5;

│h y = 2 - x 6 + 5│ - 3;
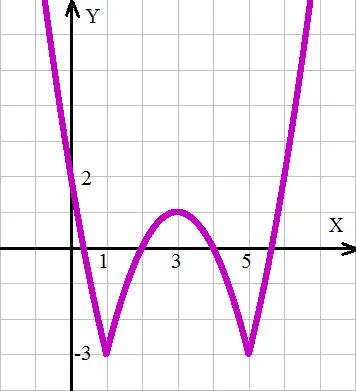
│h│ y = (x - 6) + 5;

y = h│h - 6│ + 5;
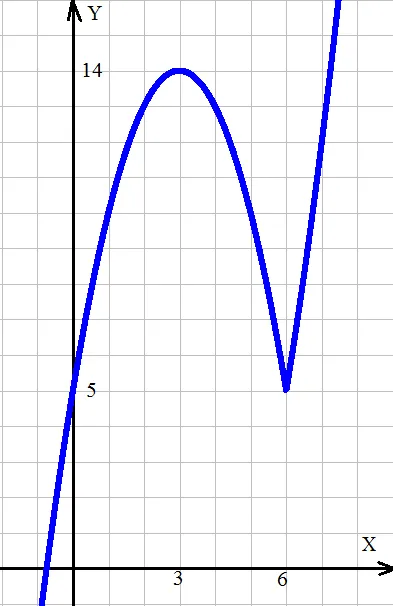
y = │h 2 - 5x + │h - 3││;

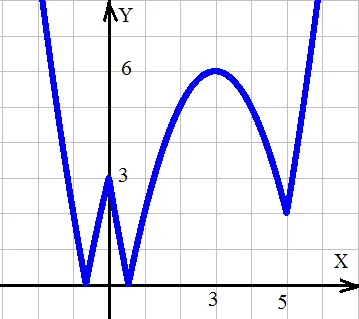
y = │h - 2│ (│h│ - 3) - 3.
V. Rezumatul rezultatelor și lecții de clasificare:
VI. Mesaj temele:
Constructul graficele funcțiilor: