fundații științifice și metodologice pentru studiul zonelor de figuri plane în școala primară, bazele teoriei spațiului

Bazele teoriei spațiului

Luați în considerare prevederile de bază ale teoriei spațiului.

Vom începe cu o zonă de definire a unui poligon. Un poligon simplu se numește linie poligonală închisă simplu, cu o porțiune a planului delimitat de acesta. Vom lua în considerare doar poligoane simplu, numindu-le pentru poligoane scurte.

Definiție: Luați în considerare mulțimea M a tuturor poligoanelor în planul euclidian. Se spune că măsurarea setului de spațiu poligoane dacă mapping definită S. M> R +. îndeplinește următoarele axiome:

Dacă poligoane F și F 'sunt egale, atunci S (F) = S (F').

S (P0) = 1. unde P0 - pătrat, construit pe intervalul unitate ca parte.

Un număr pozitiv S (F), sau măsură se numește o suprafață a unui poligon F, P0 pătrat - pătrat unitate și axiome 1, 2 și 3 - măsurare zona axiome.

Teorema 1: (existenta si unicitate): Geometria euclidiană întotdeauna există mapare S. M> R +. satisface axiomele 1, 2 și 3, iar dacă intervalul unitate selectată, atunci este o cartografiere unic.

Impact: Suma ariilor acestor triunghiuri este aceeași cu orice metoda F poligon se descompune într-un set finit de triunghiuri.

Notă: Existența și unicitatea zonei unui poligon nu este dovedit a fi în curs de geometrie școală. Cu toate acestea, teoria spațiului, predată în școli, are un înțeles specific: ea se bazează pe afirmația (care este acceptată fără dovezi) că există o mapare S. M> R +. axiome satisfacatoare 1, 2 și 3, face posibil să se calculeze aria poligoane elementare pentru anumite date, și, astfel, în poligoanele mai simplă măsură de unicitate set geometrie curs școlar. Să presupunem, de exemplu, pentru a calcula aria unui poligon F, am pătruns în triunghiuri și a luat suma ariilor triunghiurilor rezultate. Se înțelege că, în moduri diferite de divizare în triunghiuri vom obține același rezultat. Dar de ce? În școală geometrie răspuns la această întrebare este nu. Existența și teorema de unicitate dă un răspuns clar: pentru orice partiție a poligonului triunghiuri de pe F suma pătratelor dă un număr unic determinat de S (F). Din această teoremă, iar zona de ieșire din axioma formula de calcul suprafața fiecărui dreptunghi, un paralelogram, un triunghi.

Teorema 2: Dacă S. M> R + - cartografiere axiome satisfacatoare 1, 2 și 3, S (P) = xy, unde P - dreptunghi ale cărui laturi sunt egale cu x și y.

Teorema 3 Dacă S. M> R + - cartografierea axiome satisfacatoare 1, 2 și 3, S (T) = xy, unde T - triunghi, x - una din laturile sale, și y - înălțimea potrivită.

Definiție: Două poligoane sunt numite izometrică, în cazul în care zonele lor sunt egale.

Este clar că există o relație egală-echivalență pe mulțimea M a tuturor poligoanelor.

Definiție: Două poligoane F și F „se numesc equidecomposable în cazul în care acestea pot fi împărțite în același număr de poligoane, respectiv, egale.

Se poate demonstra că equidecomposability raportul de asemenea, este o relație de echivalență pe mulțimea M a tuturor poligoanelor.

Teorema 4: În cazul în care poligoanele sunt equi, au arii egale.

Notă: Această teoremă se bazează metoda de descompunere pentru calcularea suprafeței de poligon F: poligon este descompus într-un set finit de poligoane, astfel încât poate fi „pliat“ un poligon a cărui suprafață este cunoscută pentru. În acest fel, într-un curs de geometrie școală sunt formule de calcul aria unui paralelogram, un triunghi, un trapez.

Următoarea declarație este inversul Teorema 4.

Teorema 5 (Bolyai-Gervin): În cazul în care poligoanelor de suprafață egală, ei equi.

Astfel, într-o pluralitate de M egalității tuturor raport poligoane coincide cu raportul equidecomposability.

Și ce despre zona unei forme arbitrare, de exemplu, cu o suprafata de cerc? Această problemă apare atunci când geometria materialului prezentat de către școală. Există necesitatea de a extinde teoria pătrate zona de studiu, care până acum a fost doar mulțimea tuturor poligoanelor plan.

Definiție: Figura M se numește cuadratură dacă pentru orice număr pozitiv poate ridica astfel de poligon P și Q, care P și Q M S (Q) -S (P).

Teorema 6: există setul de cifre squarable, și numai una, funcția S, satisface axiome 1, 2 și 3 ale zonelor de măsurare.

Numărul de S (F) se numește aria figurii F, unde F- figura squarable.

Notă: Metoda de calcul a zonei a figurii, bazată pe luarea în considerare a poligoane, umple treptat întreaga figură, se numește metoda de epuizare (în manualele școlare cu ajutorul acestei metode obținem o formulă de calcul aria unui cerc și nu numai).

La aplicarea paleti (zone de măsurare directă).

Se spune de obicei că zona de S (F) F este numărul de cifre care indică modul în care este desenată multe unități de suprafață din această cifră (per unitate de suprafață este luată pătrată a cărei lungime este egală cu unu). Cu toate acestea, o astfel de explicație clară nu poate fi o definiție matematică precisă a conceptului de spațiu. Nu este clar, de exemplu, modul în care este compusă din unități de cerc suprafață de rază dată.

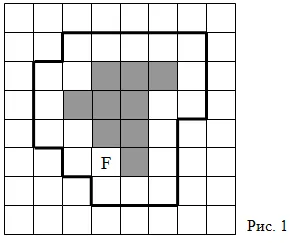
O modalitate de a determina conceptul zonei se bazează pe luarea în considerare a paletelor - partiție a planului în pătrate congruente. Lăsați partea mozaic pătrat are o lungime 1. Să se dea o cifră de F și lasă-a1 este cel mai mare număr de pătrate, conținută în întregime în figura F și B1 - cel mai mic număr de pătrate care conțin această cifră în întregime. De exemplu, figura F cuprinde o cifră formată din 9 pătrate mozaic și conținute în figură, care constă din 29 de pătrate, cu toate acestea 9 # 63; S (F) # 63; 29, și anume, a1 = 9, b1 = 29 (Fig.1).

Pentru o evaluare mai precisă poate fi utilizat paleți, care pătrate au laturile de o lungime de 1/10 (astfel încât, în fiecare pătrat 100 conține pătrate mozaic anterioare nou mozaic). Dacă, să zicem, F conține o cifră formată din 1 716 noi piețe mozaic și conținute într-o cifră formată din 1 925 din aceste pătrate, apoi 17.16 # 63; S (F) # 63; 19.25. Încă o dată, măcinare mozaic (adică, reducerea la 10 ori lungimea laturilor pătratelor), putem estima mai precis S (F), etc.

proces de măsurare descrisă este folosit nu numai pentru a găsi zona, dar, de asemenea, pentru definirea zonei. Și anume, să ia în considerare mozaic, în care lungimea laturilor pătrate sunt egale cu 1/10 k. Să presupunem că F conține o cifră formată din pătrate ak acest mozaic și conținut într-o figură alcătuită din bk acestor pătrate (de exemplu, mai sus avem a2 = 1716, b2 = 1925). Apoi, putem spune că ak / 10 2k este valoarea figura F cu o lipsă de spațiu, și bk / 10 2k - din abundență. Nelimitat k tot mai putem vedea limitele: (F) =. (F) =. prima dintre care este numit un fund, iar al doilea - zona superioară a figurii F.

În cazul în care forma este de așa natură încât aceste limite coincid cu. o cifră F este Quadrature, adică (F) = (F). Această valoare este considerată în afara zonei numită figura F și este notat cu S (F), adică

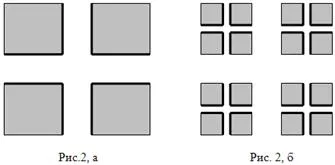
Este ușor de a da un exemplu de figuri, în care zonele superioare și inferioare nu sunt aceleași. În acest scop, suprafața de cruce pătrat elimina 1, suprafață este mai mică de 1/4 (Fig. 2a). Apoi, în fiecare din cele patru pătrate rămase să fie eliminate prin cruce, astfel încât suma suprafețelor tuturor celor patru cruci a fost mai mică decât 1/8 (fig. 2b). Apoi îndepărtați 16 cruci cu o suprafață totală mai mică de 1/16, etc. Figura care rămâne după îndepărtarea unui număr infinit de cruci, notat cu Q. De notat că suprafața totală a tuturor la distanță traversează mai puțin de 1/4 + 1/8 + 1/16 + ... + 1/2 n + ..., adică mai puțin de 1/2.

Prin urmare, cifra rămasă Q nu poate fi plasată în zona figurii 1/2, adică, figura Q zona superioară este mai mare de 1/2. În același timp, cifra de Q nu conține nici un pătrat (oricât de mică ar putea fi), și pentru că zona inferioară a figurii este zero. Astfel, zona superioară și inferioară a figurii nu coincid, și, prin urmare, nekvadriruema figura Q.

Acest exemplu arată că noțiunea de spațiu nu se aplică nici o cifră. Cu toate acestea, se poate arăta că fiecare poligon este squarability figura. De asemenea, orice formă convexă (de exemplu, cerc) squarable. Și, în general, cifrele squarable de clasă este destul de vastă.

Acum se poate spune că spațiul de măsurare S este o funcție definită pe clasa tuturor cifrelor și squarable primesc valori numerice, adică Zona S (F) din figura F este un număr nenegativ (unitate de suprafață fixă ​​presupus).

Folosind acest domeniu definiție (prin paletok) se poate dovedi un număr de proprietăți pătrat ...

În general, trebuie remarcat faptul că atunci când se utilizează paleți în școală este util să ne amintim următoarele:

Zona măsură prin mozaic este (imediat) măsurarea directă, prin valoarea dorită a cantității este determinată prin compararea acestuia cu unitatea corespunzătoare. Măsurarea suprafeței prin măsurarea lungimii segmentelor și utilizarea unei formule indirecte. Înlocuirea comparație directă comparație indirectă este o realizare semnificativă a gândirii umane și este una dintre cele mai vechi abstracțiuni matematice. Nu există nici un motiv să se presupună că această abstracție este ușor de dat de student, neînțelegere faptul complică foarte mult studiul în continuare a teoriei zonelor de măsurare (de exemplu, cea mai puțin medie dreptunghi pătrat formula de studiu pentru cazul în care lățimea și lungimea nu pot fi exprimate prin numere naturale). La urma urmei, înainte de a putea calcula lungimea segmentelor pentru orice formule predăm segmente de măsurare directă și să dea astfel o oportunitate de a testa calcul prin măsurarea directă. În subiect „Piața“, această etapă primară corespunde tocmai pentru a lucra cu palete.

Cursul geometriei spațiului limitat școlar de bază găsirea de forme cu contururi rectilinii sau circulare și părțile sale. În practică, cu toate acestea, se poate întâlni figura cu un contur arbitrar, și deranjat că absolvent de școală de bază este pregătită pentru soluționarea problemei corespunzătoare.