efect Gibbs

Principiul aproximări succesive la forma originală în mod clar vizibile în modelul grafic inferior. De asemenea, poate fi văzut, și cauzele fluctuațiilor în reconstrucția salturi ale funcțiilor, care sunt numite efectul Gibbs. Dacă modificați numărul de termeni din seria a rezumat efect Gibbs nu dispare. Nu se schimbă fluctuațiile relative de amplitudine (în raport cu amplitudinea șocului) și de atenuare relativă (la o rată de scădere treptată a fluctuațiilor amplitudine cu privire la eliberarea maximă) se modifică numai frecvența pulsațiilor, frecvența, care este determinată de ultimele armonici însumate.

Gibbs efect apare întotdeauna când încălcări grave ale funcțiilor monotone. La cursa efectul este maxim, în toate celelalte cazuri, amplitudinea pulsații depinde de natura încălcării monotonă. Un exemplu al fenomenului Gibbs pentru pulsul radio este prezentat în Fig. 4.6 (program folosit în Fig. 4.4 prezintă punctele de semnal refăcute cu creșterea scară de 10).

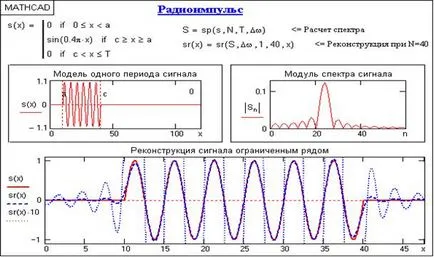
Fig. 4.7 prezintă un exemplu de forma unei serii Fourier a unei perioade de T = (a, c) modelarea SQ periodică a semnalului (x), reprezentat de semnalul de informație s (x) în suma cu un semnal de zgomot. Spectrul de zgomot similar cu spectrul de zgomot alb (zgomot al unei distribuții uniforme asupra spectrului de frecvențe de energie).

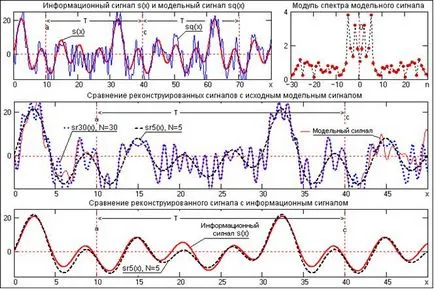
În semnal de modelare informații spectrului de frecvențe a semnalului este destul de clar alocat. semnal Reconstructia număr limitat de armonici Fourier numai de semnal informație (SR5 semnal (x), N = 5) dă o undă netezită de medie minimă discrepanță pătrat cu semnalul model pentru un anumit număr de termeni ai seriei, ci numai pe perioada de expansiune (a, c) și cea mai precisă aproximare a semnalului de informație. Odată cu creșterea numărului de reconstrucție în seria Fourier reconstruită semnalul începe să se apropie de semnalul de model, dar numai pe perioada T = (a, c), în care discrepanța semnalului crește informații. Rețineți că spectrul semnalului poate fi determinată și mai multe perioade de semnal, ceea ce crește precizia de reconstrucție a semnalului de informație.

Seria Fourier se poate descompune și funcția periodică arbitrară definită (cut mărginită de la un alt semnal, etc.) în intervalul (a, b), dacă nu suntem interesați în comportamentul său în afara intervalului. Cu toate acestea, trebuie amintit că utilizarea (4,1-4,6) automată înseamnă extensie periodică a acestei caracteristici în afara intervalului predeterminat (în fiecare parte a acestuia), cu o perioadă T = b-o. Astfel, pe fenomenul Gibbs poate să apară margini fantă dacă semnalul de sare la marginile nivelului semnalului nu se potrivește și format la repetarea periodică, așa cum se arată în Fig. 4.8. Atunci când extinderea funcției inițiale într-un număr limitat de Fourier și prelucrarea acestuia în domeniul de frecvență este, de fapt procesate în același timp, nu funcția inițială, și reconstruit dintr-un număr limitat de Fourier.

Trunchierea seriei Fourier de funcții de distorsiune definite există întotdeauna. Dar, la porțiunea joasă cut-off de proporția de energie de semnal (cu funcțiile rapide spectrele de atenuare), acest efect poate fi greu de a discerne. La rasele și discontinuități se manifestă cel mai clar.

Pagina generata pentru: 0,006 sec.