Deplasarea centrului de masă - studopediya
Punctul C poziția care este determinată de raza vectorului:
Acesta a numit centrul de masă al unui sistem. În cazul în care mi - masa de particule i-lea; vector raza definind poziția particulei - ri; - masa totală a sistemului. (Rețineți că un câmp uniform forță a centrului de greutate al masei coincide cu centrul de greutate al sistemului.)
RC Diferențierea în ceea ce privește timpul, găsiți centrul de viteza de masă:
unde Vi - viteza i-lea punct material, pi - impulsul său, P - pulsul unui sistem. Din (2.18) rezultă că impulsul total al sistemului este,
Din (2.19) și (2.16), obținem ecuația de mișcare a centrului de masă:
(Ac - accelerare a centrului de masă). Astfel, din ecuația
Rezultă că centrul de greutate se deplasează astfel încât să deplaseze punctul de material de masă egală cu masa sistemului, sub acțiunea rezultanta forțelor exterioare aplicate organelor sistemului. Pentru un sistem închis AC = 0. Aceasta înseamnă că centrul de masă al sistemului închis se deplasează uniform sau în repaus.
Un sistem de referință în raport cu care centrul de masă este în repaus, numit centrul sistemului de masă (prescurtat ts- sistem). Acest sistem este un sistem inerțial.
1. Care rame legile lui Newton sunt valabile?
2. Care sunt formularea a doua lege a lui Newton, știi?
3. Care este greutatea unui corp în cădere liberă?
4. Care este semnul produsului scalar al forței de frecare și a vitezei corpului?
5. Care este impulsul unui sistem CMS?
6. Care este accelerația centrului de masă al corpului având o masă m, și sub acțiunea forțelor?
1. Glonțul perforeze doua cutie contigue cu lichide: mai întâi cutia cu glicerol și apoi aceeași cutie cu apă. Cum va viteza finală a glonțului, în cazul în care caseta pentru a schimba? Alte forțe care acționează asupra glonțului, în plus, forța de rezistență lichidă F = -rV. neglijat.
2. Mișcarea punctului material definit de ecuațiile x = la 3. y = bt. dacă forța variază, care acționează asupra punctului: a) pentru modulul; b) în direcția?
3. Viteza punctului material dat de ecuațiile ux = A # 8729; sinwt, uy = A # 8729; coswt. dacă forța variază, care acționează asupra punctului: a) pentru modulul; b) în direcția?
4. Mingea agățat de lungimea firului l. după situată pe o forță orizontală, înălțimea H. fără să se miște circumferențial. Poate viteza sa fie zero: a) H
5. Două m1 de masă corporală> m2 cad de la aceeași înălțime. forțelor de rezistență presupune a fi constantă și aceeași pentru ambele organisme. Comparați căderea corpurilor.
6. Două bar identic asociat fir, se deplasează pe un plan orizontal sub influența forțelor orizontale F. Este forța de tensionare a firului depinde: a) greutatea barelor; b) pe barele ale coeficientului de frecare pe planul?
7. O masă bar m1 = 1 kg greutate se sprijină pe bara de m2 = 2 kg. Pe bara orizontală inferioară începe să acționeze o forță crescând liniar cu timpul, modulul său F = 3t (F - în H, t - V s). La un moment dat în timp bara de sus începe să alunece? Coeficientul de frecare dintre barele m = 0,1, frecarea dintre bara de jos, iar suportul este neglijabil. Ia g = 10 m / s 2.
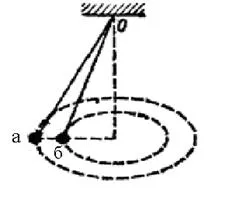
8. Două bile și b, suspendat pe un total de filamente tochke0, mișcă uniform de-a lungul căilor circulare care se află în același plan orizontal. Comparați vitezele unghiulare ale acestora.
9. Buncărul conic este rotit la o greutate constantă de viteză unghiulară. În interiorul craterului se află pe peretele corpului, care este liber să alunece de-a lungul conului. Când corpul rotativ este în echilibru în raport cu peretele. Este acest echilibru stabil sau instabil?