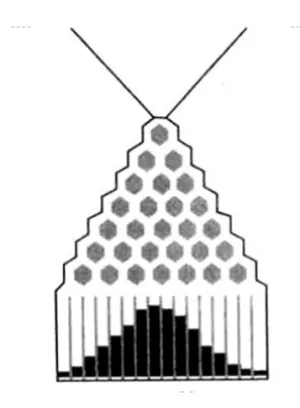
curba Gauss
Baza de asociere de probabilitate și statistici sunt două fapte remarcabile. Unul dintre ei - un fenomen de stabilitate statistică. Al doilea este că în multe, diverse observări statistice inerent stabilitate statistică poate fi descrisă printr-o singură funcție. Această caracteristică a fost introdusă de către marele matematician german Karlom Gaussom (\ (1777-1855 \)). Ea este dată o formulă foarte complicat:
ϕ (X) = 1 luna februarie π e - x 2 luna februarie
Graficul y = ϕ (X), numit o curbă Gauss. Aceasta este o „formă de clopot“ curba. Are un singur simetric punct maxim în raport cu axa ordonată, aria de sub curba egală cu unitatea. Ea repede se apropie asimptotic axa x:
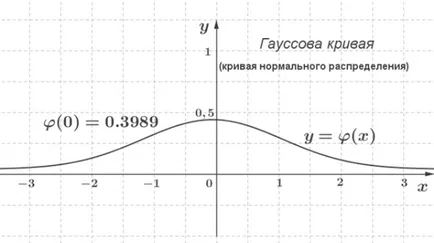
Esli estimează aria de sub curba gaussiană în intervalul - 3; 3. veți obține un \ (0,99 \), t. E. Mai mult de 99% din suprafața.
Histogramele distribuției unei cantități mari de informații sunt indispensabile în cazurile în care numărul de date constă dintr-un număr foarte mare de numere. Dacă lățimea coloanelor verticale ale histogramei este suficient de mică, iar baza coloanei, în asociere a permis un anumit interval de timp, atunci histograma este ea însăși similar cu graficul unei funcții continue definite pe acest interval. Uneori, această funcție este numită o funcție de nivelare.
Histograma funcții de egalizare similare între ele. Toate aceste curbe de distribuție obținute din curba Gauss. Acesta este adesea numit curba de distribuție normală.
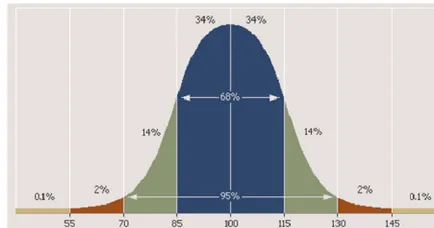
Pentru a demonstra acțiunea legii de distribuție Gauss, uneori, folosesc un dispozitiv special - un consiliu Galton (numit după inventatorul său). În ea rulare în partea de sus a acelorași bile sunt distribuite pe mișcă între un hexagon regulat, ca urmare a căderii pe o suprafață orizontală, formând o imagine similară cu „subgrafic“ curba clopot: