Consolidarea plăților - studopediya
Pentru a crește capacitatea și o reducere de numerar pot fi aplicate diferite tipuri de rate ale dobânzii. Este adesea necesar pentru a determina ratele, care conduc la aceleași rezultate financiare în condiții specifice, atunci când înlocuiți un tip de pariu pe de altă parte, sub rezerva principiului echivalenței nu schimbă relațiile financiare dintre părți într-o singură operațiune.
Ratele dobânzilor, care oferă aceleași consecințe financiare nazyvayutsyaekvivalentnymi. Echivalența ratei furnizate de multiplicatori de ecuații ale amestecului sau a factorilor de actualizare.
Tabelul 3.1 - Echivalența ratelor dobânzii
Termenul tranzacției exprimat în ani (n)
timp de tranzacții, exprimat în luni (m)
Termenul tranzacției este exprimat în zile (baza de timp pentru ambele rate la 360 de zile)
Termenul tranzacției este exprimat în zile (baza de timp pentru rata dobânzii de 365 de zile și 360 de zile, rata dobânzii)
Continuare Tabelul 3.1
Exemplul 3.1 Un instrument este considerat pentru anul anterior datei de rambursare la o rată de reducere de 15,0%. Care este profitabilitatea contului operațiunilor sub formă de rate ale dobânzii?
Conform formulei 3.1 găsim:
Exemplul 3.2 Care este rata anuală de dificilă în contract poate fi înlocuită cu o cotă unică de 18% (K = 365), fără a schimba implicațiile financiare? Termenul de funcționare de 580 de zile.
Am găsit echivalentul unui pariu complex prin formula 3.9
Exemplul 3.3 În dezvoltarea condițiilor contractului părțile au convenit că rentabilitatea împrumutului este de 28% pe an. Care ar trebui să fie de mărimea ratei nominale a dobânzii, atunci când lunar, trimestrial?
3.20 folosește formula:
; .
În cazul în care rata dobânzii tranzacțiile financiare variază în timp, toate ratele de valori pot fi generalizate folosind media.
Să presupunem pentru perioadele acumulate rate ale dobânzii simple.
Rata medie se obține prin echivalarea factorilor corespunzători compoundare unul de altul:
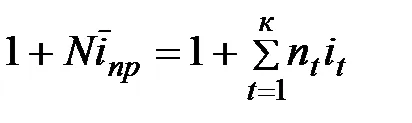
În mod similar, obținem
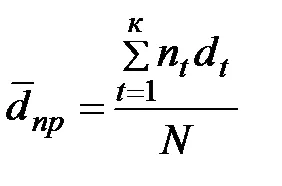
unde N = - perioada totală a dobânzilor acumulate,
și - contul de mediu și rata dobânzii.
În cazul în care schimbarea în timp și suma inițială,
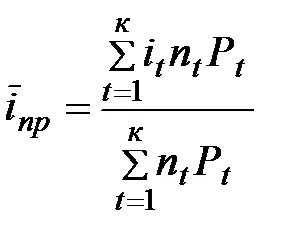
Dacă rata de timp care variază în medie de interes compus, atunci:
Exemplul 3.4 Pentru primii doi ani ai creditului rată de 20% aplicat pentru următorii trei ani, este de 24%. Trebuie să găsim rata medie.
0.22384 sau 22.384%.
Uneori doar schimbarea suma creditului și dobânda, iar termenii sunt operațiuni.
Dacă aplicați interes simplă,
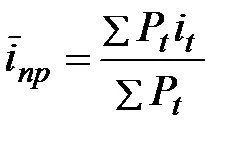
Atunci când rata dobânzii medie complexă, rata medie va fi
De multe ori este necesar să se modifice condițiile de tranzacții anterioare: modificări în calendarul de plăți, se combină mai multe plăți într-una singură - plățile de consolidare.
Să scadente înlocuit cu unul în suma și scadența. În acest caz, există două formulări posibile ale problemei: în cazul în care perioada specificată. este suma. Pe de altă parte, dacă setați valoarea plății consolidate este determinată de viața sa.
Determinarea dimensiunii plății.
1) Dacă utilizați o rată a dobânzii simple și condițiile de plată este mai mică decât termenul de plată unită consolidată,
în cazul în care - dimensiunea unit cu termenii de plată <.
2) Dacă utilizați o rată a dobânzii și simplu termenii de plată uniți atât mai puțin și mai mult termenul de plată consolidate,
în cazul în care Sj - suma de plăți cu scadențe nj
3) Dacă utilizați o rată de actualizare simplă și calendarul plăților mai puțin unite termenul limită de plată consolidate,
4) Dacă folosiți o rată de actualizare simplă și calendarul de plăți unite atât mai puțin și mai mult termenul de plată consolidate,
5) Dacă utilizați o rată a dobânzii complexă și condițiile de plată este mai mică decât termenul unit plată consolidată:
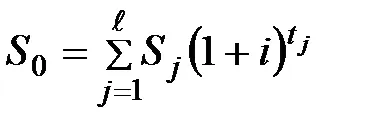
6) În cazul în care aveți o rată a dobânzii dificilă și condițiile de plată unite, atât pe termen de plată mai puțin și mai consolidate:
. atunci când Nj 7) Dacă utilizați o rată de actualizare complexă și calendarul plăților mai puțin unite termenul limită de plată consolidate, 8) Dacă aveți o rată de actualizare dificilă și calendarul plăților unite atât mai puțin și mai mult pe termen de plată consolidate: Definiția plății consolidate pe termen lung. La calcularea perioadei dobânzii simplu nici o plată consolidată este dată de: în cazul în care P0 - valoarea actuală a plății consolidate Când se utilizează de compunere: Echivalare discrete complex și rata continuă. Notăm puterea prin creștere - b. Echivalența ratei dobânzii complexe și vigoare: Echivalența rata nominală a dobânzii și creșterea forțelor: Echivalența rate de creștere și de interes: