comparații de sistem, comparații de primul grad al sistemului - metoda teoriei comparație

comparații sistem de gradul I

comparații sistem de gradul I cu același necunoscut, dar cu diferite module scrise într-o formă generală, după cum urmează:

Metoda generală (Metoda soluții succesive) este că prima este o primă comparație, în care: - cea mai mică sau cea mai mică nenegative reziduuri absolut numerele modulo și beretsyaklass

satisfăcătoare decât prima.

Această valoare este apoi înlocuit în al doilea chtodaet comparație

unde este din nou într-o clasă de numere este substituit în ecuația (.

Rezultatul este o valoare într-un număr de clasă care îndeplinesc primul sistem de două comparații. Apoi, această valoare este substituit în a treia comparație a sistemului, așa cum este, și este apoi înlocuit în al patrulea sistem de comparație, etc.

Rețineți că este posibil să meargă într-un mod oarecum diferit: comparații în primul rând, fiecare dintre sistemul este realizat și este reprezentat ca:

și primește apoi modul descris.

Dacă se dovedește că cel puțin una dintre comparații de sistem (4.1) nu are nici o soluție sau o comparație în ceea ce privește metoda descrisă nu poate fi rezolvată, atunci sistemul (4.1) nu are nici o soluție.

Dacă sistemul de congruentelor (4.1) și elementul de tăiere și modulul de fiecare comparație, obținem sistemul:

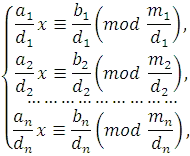
Comparațiile acestui sistem poate fi rezolvată pentru a reduce și soluția sistemului (4.3) la soluție:

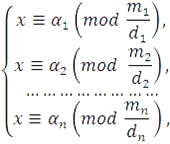
Daca sistemul (4.2) module în perechi simple, soluția este posibil să se găsească nu obschimsposobom cele de mai sus, și în conformitate cu formula:

în cazul în care există decizii de comparații:

soluția sistemului este:

Această metodă se poate rezolva sistemul (4.4), în cazul în care modulele sunt mutual prime.

Exemplul 1: rezolva sistemul de comparatii:

clase de reziduuri. dacă avem:

1). în consecință, satisface primul sistem comparație,

2). prin urmare, acesta îndeplinește al doilea sistem de comparație.

Prin urmare, clasa de reziduuri este o soluție. Puteți înregistra clasa un mod diferit: prin adăugarea la unitatea de 9, constatăm că

Deci, acest sistem are o soluție de comparații