Suprafața unei figuri plate în coordonate polare calculul volumelor corpurilor - rezolvarea problemelor de control

formă plată pătrată în coordonate polare Calculul volumelor corpurilor

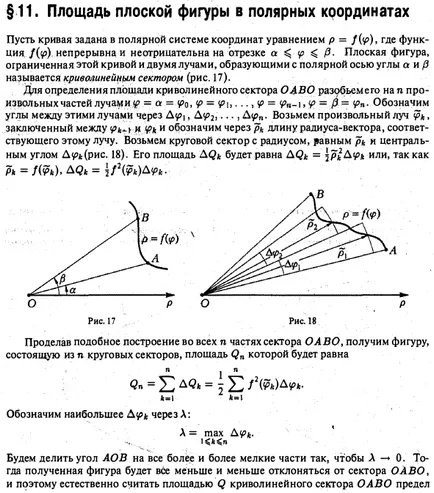
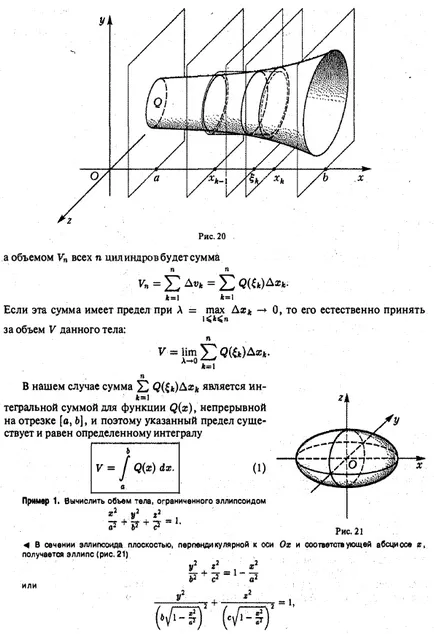
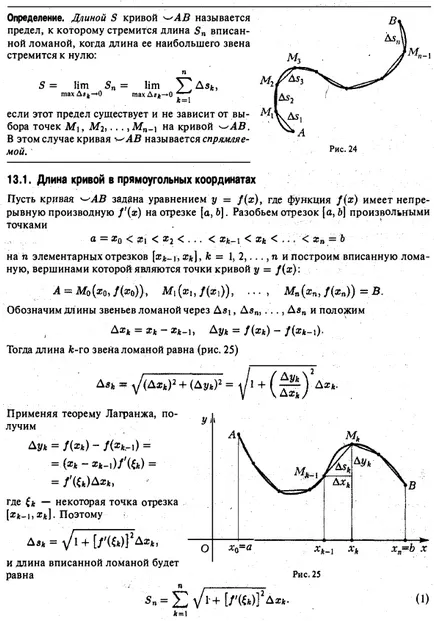
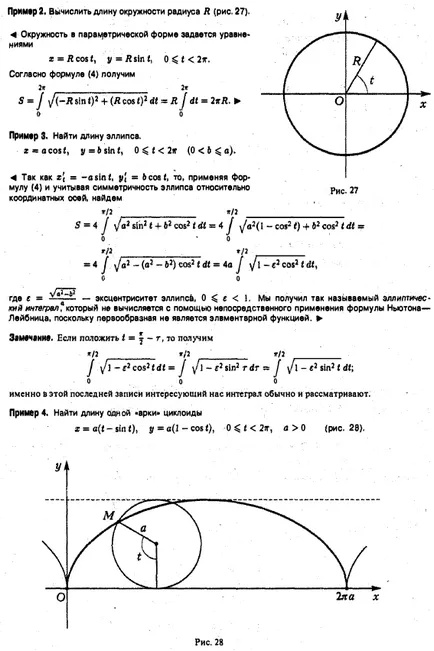
Fie curba este dată de ecuația în sistemul de coordonate polare. în cazul în care funcția este continuă și nenegativ pe intervalul. O figură plană delimitată de această curbă și cele două fascicule care formează cu axa polară a unghiurilor a și (5 numitul sector curbat (Fig. 17). Pentru a determina aria curbat razobsmsgo sectorului OAVO în părți arbitrare n razele n indica unghiurile dintre razele prin a lua un arbitrar grinda închisă între și reprezintă lungimea pk a vectorului raza corespunzătoare fasciculului. să considerăm un sector circular cu o rază egală cu pk și un unghi central de Ay> * (Fig. 18). zona AQk sa este egală sau, ca pk = Fig. 18 Făcând astfel va construi ix toate n părți din sectorul INFORMAȚII obține o cifră constând în n sectoare de cerc, zona Qn care este egală pentru a desemna cea mai mare prin L: formă plată pătrat în coordonate polare de calcul corpuri volume lungime curba lungimii de calcul dreptunghiulare coordonate lungimea curbei a curbei definită de în formă parametrică a curbei lungime coordonate polare Impartim unghiul B al AO piese din ce în ce mai mici, astfel încât 0. Apoi, cifra rezultată ar fi deviaza mai puțin din sectorul OAVO și, prin urmare firesc să-și asume zona Q a curbata limita sectorului OAVO Cn construit figuri fac o greșeală atunci când. cu condiția că există această limită și nu depinde de modul în care segmentul de partiție [a, p) în segmente parțiale, iar punctele de alegere pentru ei. Astfel, prin definiție, avem 1 Suma 2 este funcția suma integrală care este continuă pe intervalul [a, (5 \ prin continuitatea funcției / (y?). Prin urmare, această sumă atunci când A G are o limită egală definit integral F 2M df . Astfel, suprafața sectorului curbat este OAVO Exemplul 1. Găsiți aria figurii delimitată de zona de căutare cardioid .2 2 «§ 12. Calcularea volumelor corpurilor Luati in considerare corp delimitat de o suprafață închisă. Fie Q zona cunoscută a oricărui plan corp în secțiune perpendiculară pe axa oh . Această zonă depinde de poziția planului de tăiere, adică este o funcție de x (Figura 20).: .. Presupunem că funcția este continuă pe intervalul [a, b). Pentru a determina domeniul de aplicare al planului de efectuare a corpului. care razobyuttelo în n straturi. In fiecare interval [x, n, luați la un punct arbitrar; k și înlocuiți fiecare corp de cilindru strat cu generatoarele paralele cu axa Ox, ghidul care este o secțiune a conturului corpului planul x = (k (Figura 20) Volumul Avk astfel cilindru este .. produs al zonei în care e bazei sale prin înălțimea Akhk :. și volumul V „toți cilindrii n va fi suma de la 0, este firesc să ia =) fc = i Dacă această sumă are o limită ca = max Da * pentru volumul V al corpului? : În acest caz, cantitatea de 2 este de o valoare integrală a Q funcția (x), continuă pe intervalul [a, 6], iar poetul CB specificate limită și există o integrală certă din exemplul 1. Se calculează volumul corpului delimitat de o dimensiune elipsoid plan figura r2 în polar Calculul coordonatelor Calcularea lungimii volumelor corpului lungimea curbei a curbei dreptunghiulare coordonate lungimea curbei specificată în lungimea formei parametrică a curbei în coordonate polare în secțiunea 4 elipsoid printr-un plan perpendicular pe axa x și abscisa corespunzătoare obțin o elipsă (Fig. 21) sau semiaxa care sunt Q zona -Therefore (x) este egală cu secțiunea transversală Aplicarea formulei (1), obținem în particular, când elipsoidului este tras într-o sferă. iar volumul este egal Să considerăm un corp format prin rotirea în jurul axei Ox ava curbat trapezoid (Fig. 22), delimitată de curba y = f (x) y Ox și drepte. Acest organism este numit corpul de revoluție. planul de rotație al secțiunii de corp, perpendicular pe axa x și corespunzând abscisă x, pătrat este un cerc. prin urmare, cantitatea de rotație a corpului 4 Ecuația parabolei este OA arc. Volumul Căutând este §13. Calcularea lungimii EXEMPLUL curbei 2. Găsiți volumul corpului de rotație obținut prin rotirea unui arc de parabole OA y2 = 2px în jurul axei Ox (fig.23). Fig.23 Luați în considerare curba ^ AB având capetele de la punctele A și B, și l-am lua pentru punct arbitrar M \. ca urmare a lungul curbei, una după alta (fig. 24). Conectați aceste puncte polifonice .dliny care sunt notate cu. Apoi, lungimea Sn a liniei rupte. înscrisă în curba ^ AB, va fi egală cu definiție. Lungimea S ^ AB a curbei este limita la care tinde lungime 5 „poligonului înscris atunci când lungimea de nivelul său maxim de la zero: în cazul în care există această limită și nu depinde de alegerea punctelor de pe curba, în acest caz, curba ^ AB numit care se poate rectifica. „Fig. 24 13.1. Lungimea în coordonatele rectangulare Wav curba Să presupunem că curba definită de ecuația y = f (x) y unde f (x) funcția are un derivat continuu / „(x) pe [a, b]. Se împarte intervalul [a, puncte arbitrare în intervale elementare n și ATG constructelor inscripționată vârfuri polilinii din care sunt puncte de pe curba y = / (I): ins Notam Q. pentru unitățile poligonale prin PCR și apoi setați link-ul de lungime fc-ro este poligonală (Figura . 25) Utilizând teorema lui Lagrange, în care - un anumit punct al segmentului (xjk.ii «JK). Prin urmare, lungimea poligonului inscris este egal Deoarece starea f „(x) este continua pe [a, 6], funcția este continuă în acest interval și, prin urmare, suma integrală (1) are o limită la un S max. care este definit de integrala: sau, pe scurt, din punct de catenare ecuație găsi Considerând identitatea obține aria unei figuri plane în coordonate polare Calculând corpurile volume Calculând lungimea curbei lungimea curbei dreptunghiulare coordonate lungimea curbei specificată în forma parametrica lungimea curbei în coordonate polare De aceea EXEMPLUL 1 . Se calculează lungimea de 5 catenare. Lungimea curbei, date în formă parametrică Let ^ curba AB dată în formă parametrică în care funcțiile și ecuațiile) au derivaților continue pe segmentul. în care pe acest segment. În acest caz, ecuația (3) definesc o funcție y = / (x) având un derivat continuu pe y'x = F]. Apoi, în conformitate cu formula (2) sau Exemplul 2. Se calculează lungimea circumferința cu raza R (fig. 27). 4 Circumferință în formă parametrică dată de ecuațiilor. Conform ecuației (4) conduce la exemplul 3. Găsiți lungimea elipsei. apoi, folosind formula (4) și ținând seama de simetria elipsă în raport cu axele de coordonate, find unde „- excentricitatea eliptică. Avem așa-numitele eliptică integrale * care nu se calculează prin aplicarea directă cu formula Newton-Leibniz, deoarece primitiv nu este o funcție elementară. + Notă. Dacă pui. Ooo obținem este în această ultimă înregistrare ne interesează integralei de obicei luate în considerare. Exemplul 4. Găsiți lungime de un -arki „lungimea curbei cicloida în coordonate polare Să curba wav dată de o ecuație în coordonate polare r, unde / (y?) Are un derivat continuu) pe segmentul pentru a găsi lungimea curbei a ecuației sale parametrice. În acest scop, folosim formule de tranziție de la polare la coordonate carteziene. Substituind funcția p / (în?), Obținem ecuația. care sunt ecuațiile parametrice ale curbei. Aici, argumentul este unghiul polar y. Diferentierea ultima ecuație, găsim. Cvadratura ambele părți și adăugarea de fiecare egalitate, am Conform formulei (4), obținem sau, echivalent, (6) Exemplul 5. Lungimea Se calculează cardioidă cardioidă găsi din Eq. Aplicând formula (b), vom vedea că