Studiul funcțiilor și grafice - studopediya
Funcții complete de cercetare pentru a construi programul său include următoarele elemente (nu neapărat în această ordine).
1) Domeniul definiția funcției (OOF) și domeniul valorilor sale (OZF).
Dacă domeniul funcției nu este definită în mod specific, se consideră că acesta coincide cu intervalul de valori acceptabile ale argumentului său, și anume, multimea tuturor punctelor de x. pentru care operațiunea este f fezabilă. Când a găsi utilizarea OOF OOF funcții elementare. . . și colab.
Intervalul funcției este numai în cazurile în care se poate observa imediat, pe baza proprietăților funcțiilor elementare, de exemplu, pentru funcția. în mod evident.
2) Funcția Paritatea a frecvenței sale.
Pentru a stabili funcția de paritate (nui adevărat). având o regiune simetrică determinare de verificare a validității ecuațiile () pentru toate OOF.
În caz de paritate de studiu în funcție de comportamentul și ei pot fi grafice efectuate numai. și apoi termina graficul folosind simetria: pentru chiar simetric funcția în raport cu graficul OY axa. și pentru ciudat - despre originea.
Pentru a stabili periodicitatea verificării valabilității egalității pentru OOF, în cazul în care T este determinată de forma funcției. În cazul studiului funcției periodice efectuate pentru un interval de periodicitate.
3) Funcția de continuitate, puncte de discontinuitate, asimptota verticală.
Pentru a determina continuitatea continuității intervale funcții utilizează funcțiile elementare de bază. La punctele de „suspecte“ rupere (puncte separate, în afara OOF), continuitate condițiile de verificare de execuție. Dacă funcția este discontinuă la x0. opredelyut tipul de discontinuitate.
Dacă funcția are o discontinuitate infinit la un moment dat x0. apoi linie dreaptă x = x0 este o asimptotă verticală a graficului funcției. În cazul în care numai limite cu o singură față la x0 - x0 + 0 sau 0 este infinit, atunci asimptota se numește o singură față.
Dacă funcția nu este definită pe axa reală ansamblu, este necesar să se calculeze funcția unilaterală limite la punctele, limitând lacunele OOF. În cazul în care o limită unilaterală a funcției la punctul a. OOF delimitând diferența este infinit, atunci x = a este functii grafice asimptotă verticale unilaterale. De exemplu, în cazul în care OOF :. atunci ai nevoie pentru a găsi; în cazul în care această limită ar fi infinit, atunci x = a este asimptotă verticală funcții grafice unilaterale.
4) Lacunele monotonie și extremele.
Pentru a determina intervalele de funcții monotone folosesc un criteriu suficient pentru monotonie.
Un criteriu suficient pentru monotonia functiilor derivabile:
dacă intervalul x Î(A. B) un derivat de semn constant, funcția menține monotonia în acest interval, și anume: în cazul în care. apoi f (x) crește dacă. apoi f (x) scade.
Pentru a stabili punctele extreme ale funcțiilor folosesc condițiile necesare și suficiente pentru existența unui extremum.
O condiție necesară pentru existența funcțiilor extreme. în cazul în care o funcție continuă are un extremum la x0. derivatul său în acest punct este egal cu zero sau nu există.
Punctele care aparțin OOF în care este derivat de la zero sau nu există, sunt numite puncte critice ale funcției pe primul său derivat (puncte, „suspecte în valoare extremă“).
Primul semn al existenței unei extreme suficiente. în cazul în care modificările derivate semneze, atunci punctul x0 este valoarea extremă și acest maxim dacă modificările semn de la pozitiv la negativ, iar acest lucru este minim dacă modificările semn de la minus la plus în care trece prin punctul x0 critic (de la stânga la dreapta). Dacă trec prin derivatul critic punctul X0 nu se schimbă semnul, atunci punctul x0 nu este funcții extreme.
Al doilea criteriu suficient pentru existența extreme. în cazul în care - de două ori derivabile la x0. apoi în cazul în care. apoi X0 - punctul minim, și în cazul în care. apoi X0 - punctul maxim.
Pentru a găsi punctele extreme ale primelor funcții sunt punctele critice ale primului derivat. După aceea, verificați-le în îndeplinirea unor condiții suficiente pentru existența unor funcții extreme.
5) Intervalele de convexitate, concavitate și punctul de inflexiune al graficului.
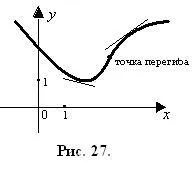
Punctele aparținând curbei, și separă porțiunile ridicate ale concavitate, numite puncte de inflexiune (Fig. 27).
condiție suficientă pentru convexitate, concavitate graficului funcției: dacă funcția este de două ori diferențiabilă și al doilea derivat al său semn constant pentru toate x Î(A, b), graficul funcției are o direcție constantă de convexitate în acest interval: a <0 – выпуклость вверх, при>0 - concavitatea (convexitatea în jos).
O condiție necesară pentru un punct de inflexiune. în cazul în care X0 - abscisa punctului de inflexiune al graficului funcției. apoi derivata a doua în acest punct este egal cu zero sau nu există.
Punctele care aparțin funcției grafice. care fie nu există, este numit puncte critice ale funcției sale (a doua derivate de puncte „suspecte pentru cot“).
condiție suficientă pentru ca un punct de inflexiune. în cazul în care derivata a doua, în care trece prin punctul x0. suspecte să se aplece, semn de schimbare, punctul de grafic cu X0 abscisa este un punct de inflexiune. În cazul în care nici o schimbare semna atunci când trece prin X0. atunci nu inflexiune.
Când a găsi intervale de convexitate, concavitatea graficului primei găsi punctele critice ale doilea derivat, apoi eliberați intervale de semn constant al doilea derivat de la OOF dacă. curba este concavă, ca și în cazul în care. curba este convexă. punctul de inflexiune este determinată folosind o condiție suficientă de inflexiune.
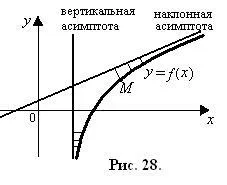
6) asimptotă înclinată și orizontală.
Asimptotă curbei având o ramură infinită numită distanță direct la care, din punctul curent al curbei M tinde la zero, ca punctul M de origine (fig. 28).
Dacă graficul are asimptota funcție înclinată cu o ecuație. parametrii k și b în ecuația asimptota pot fi găsite prin formulele:
În cazul în care cel puțin una dintre aceste limite este infinit sau nu există, atunci panta asimptota acolo. În cazul în care k = 0, graficul are o asimptotă orizontală cu y ecuație = b.
În unele cazuri (de regulă, în cazul în care f (x) este exprimată printr-o funcție exponențială sau logaritmică), programul poate avea doar asymptotes la sau numai.
Uneori, ramura grafică la și au diferite asimptota.
7) Punctele de intersecție ale graficului cu axele de coordonate sau un alt punct suplimentar pe grafic.
puncte suplimentare ale graficului sunt, în cazurile în care nu sunt suficiente informații pentru a selecta dimensiunea axelor de coordonate, adică, când un interval OOF fără puncte extreme sau puncte de inflexiune sau punctele de intersecție ale graficului cu axele de coordonate.
Antiderivative și nedefinită integrală. integralele Tabelul
Funcția (x) F se numește primitivă pentru funcția f (x) în intervalul (a. B), în cazul în care pentru toate x, egalitatea acestui interval
integrală nedefinită a funcției f (x) este multimea tuturor primitivelor functiei, adica indefinit integral - o expresie a formei. în cazul în care.
Procedura de constatare integralei nedeterminată se numește integrare. În integrarea utilizată: Tabel integral (tabelul 2), proprietățile integralelor și metode speciale de integrare, a cărui principal - înlocuirea variabilei și integrarea prin părți.
Tabelul integralelor nedefinite de bază.
1 .; 2; 3; 4; 5; 6; 7; 8; 9;
10; 11; 12; 13; 14; 15; 16.