Studiul abstract al sistemelor de control liniare și neliniare - Banca de rezumate, eseuri, prelegeri

În urma analizării datelor, putem concluziona că fiecare ATS are avantajele și dezavantajele sale. RAA cu P-regulator are cea mai mică abatere în amplitudine, dar are o eroare de statică. La PAC cu PI nu este static de eroare, dar are cel mai mare timp de control. ATS cu PID mai mare viteză, dar are, de asemenea, cea mai mare depășire.

Evaluarea calității perturbării canalului SAR

Pentru a evalua calitatea perturbației canalului SAR converti diagrama bloc ATS (Figura 8).

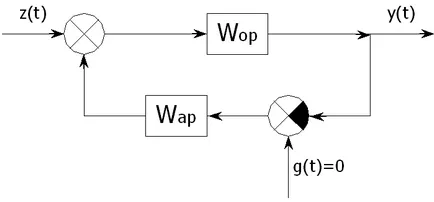
Figura 8 - Schema bloc a SAR transformat

Definim funcția de transfer al SAR pe canalul deranjant:

336 s ^ 3 + 148.4 s ^ 2 + 39.64 s + 6.859

0,9 s ^ 3 s ^ 7 + 2 + 2.2 s

336 s ^ 4 + 147.1 s ^ 3 + 29,56 s ^ 2 + 4.348 s + 0.2156

0,9 s ^ 3 s ^ 7 + 2 + 2.2 s

337,8 s ^ 4 + 162,1 s ^ 3 + 40 s ^ 2 + 6,77 s + 0.396

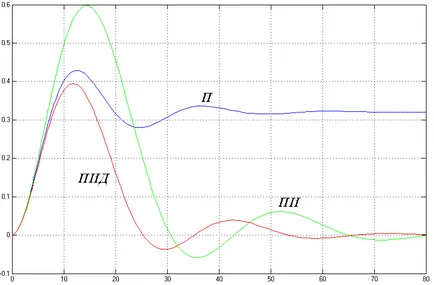
Figura 8 - Performanța tranzitorie ATS perturbații canal

Tabelul 2 - ATS Indicatori de calitate perturbație canal

După analizarea datelor, se poate concluziona că canalul ATS efecte perturbatori de la P-regulator are cea mai mică abatere în amplitudine, dar are o eroare de statică. La PAC cu PI nu este static de eroare, dar are cel mai mare timp de control. PAC cu cea mai bună performanță PID.

Evaluarea marja de stabilitate PAC

Tabelul 3 - ATS marja de stabilitate

După analiza datelor, putem concluziona că o marjă necesară de stabilitate și amplitudinea și faza au toate SAR.Otsenka controlabilitate și observabilitate liniar ATS

Analiza SAR cu P-regulator

Dezvoltarea unui model matematic al „intrare-stare-ieșire“

Funcția de transfer de bază al SAR cu P-regulator a fost obținut în Sec. 1.3. Ea are forma:

Ordinea polinomul caracteristic. Pentru aceasta ATS selecta o reprezentare canonică forma a doua controlată sau ghidat (UE). Modelul matematic este descris de către sistemul de ecuații vectoriale CAP-matrice:

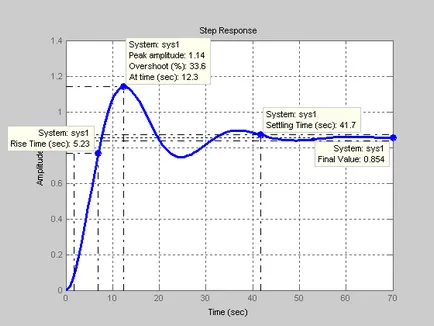
Figura 9 - Răspunsul pas la CAP P-regulator

Când au fost preparate modelul isolzovanii „input-output“ și modele „input-stare-ieșire“ exact același răspuns tranzitoriu (figurile 4 și 9), prin urmare, modelul „input-stare-ieșire“ pentru AAR cu P-regulator calculat corect.

Circuit SAR structural cu P-regulator

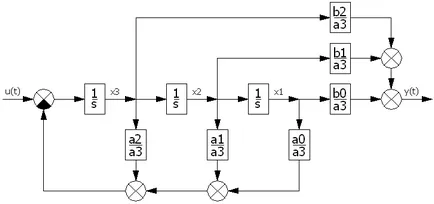
Figura 10 - Schema bloc a SAR cu P-regulator

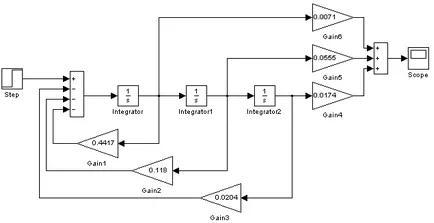
Figura 11 - Schema s model ATS cu P-regulator

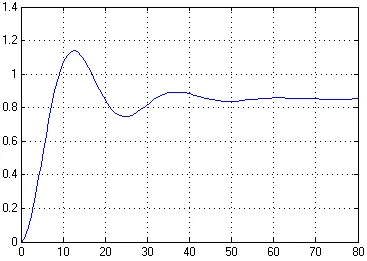
Figura 12 - Răspunsul pas la CAP P-regulator

Caracteristica tranzitorie obținută s model ATS cu P-regulator folosind sistemul pachetul MATLAB Simulink coincide cu caracteristicile de tranziție obținute anterior, apoi s-dreapta model este construit.

Calificarea ATS controlabilitatea cu regulator P

Evaluarea manipulare PAC va fi realizată cu ajutorul criteriului controlabilitate Kalman. matrice controlabilitate este după cum urmează:

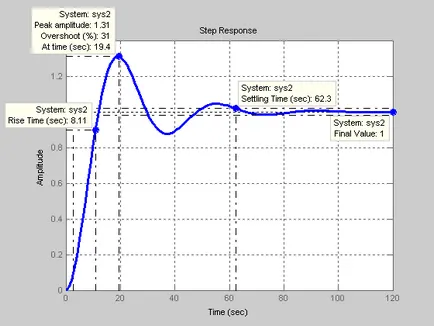
Figura 13 - Etapa CAP răspuns cu PI

Când au fost preparate exact modelul isolzovanii „input-output“ și modele „input-stare-ieșire“ același răspuns tranzitoriu (figurile 5 și 13), prin urmare, modelul „input-stare-ieșire“ pentru AAR cu PI calculat corect.

schema structurală PAC cu PI

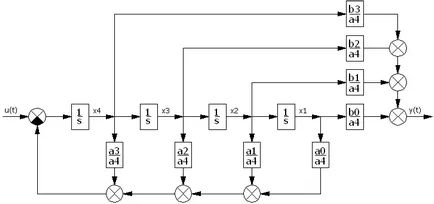
Figura 14 - Schema bloc a SAR cu PI

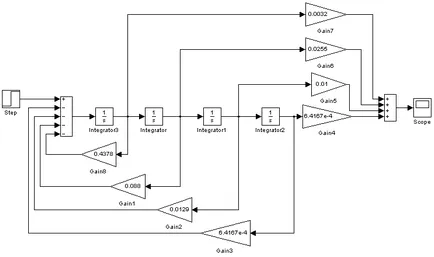
Figura 15 - Diagrama modelelor s-PAC cu PI

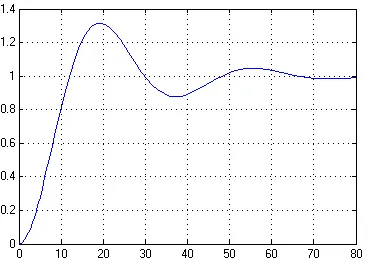
Figura 16 - Etapa CAP răspuns cu PI

răspuns tranzitoriu primit pe e-model, SAR cu PI folosind sistemul pachetul MATLAB Simulink coincide cu caracteristicile tranzitorii obținute anterior, apoi s-model este construit, dreapta.

Evaluarea PAC de manipulare cu PI

Evaluarea manipulare PAC va fi realizată cu ajutorul criteriului controlabilitate Kalman. matrice controlabilitate este după cum urmează:

>> Y2 = [B2 A2 * B2 A2 ^ 2 * B2 A2 ^ 3 * B2]

0 0 1.0000 -0.4378

0 1,0000 -0,4378 0,1037

1,0000 -0,4378 0,1037 -0,0198

Conform criteriului controlabilitatea Kalman sistemului în studiu este complet controlabile, ca matrice controlabilitate de rang egal cu mărimea vectorului variabilelor de stare. determinant matrice controlabilitate nu este zero, înseamnă că nu este degenerat. De asemenea, înseamnă că sistemul de control automat este complet controlabil.

Evaluarea observability PAC cu PI

Evaluarea PAC observabilitate va fi realizată cu ajutorul unui criteriu observabilitate Kalman. matrice observabilitate are următoarea formă:

>> H2 = [C2; C2 * A2; C2 * A2 ^ 2; C2 * A2 ^ 3]

0,0006 0,0100 0,0255 0,0032

-0,0000 0,0006 0,0097 0,0241

-0,0000 -0,0003 -0,0015 -0,0009

0,0000 -0,0000 -0,0002 -0,0011

Conform criteriului observabilitate sistemului observabil Kalman investigat complet, deoarece matricea de observabilitate de rang egal cu mărimea vectorului variabilelor de stare. determinant matrice observabilitate nu este zero, înseamnă că nu este degenerat. De asemenea, înseamnă că ACS este complet observabil.

SAR Analiza PID

Dezvoltarea unui model matematic al „intrare-stare-ieșire“

Funcția de transfer de bază al ATS cu PID a fost obținut în Sec. 1.5. Ea are forma:

Ordinea polinomul caracteristic. Modelul matematic al sistemului SAR este descris de ecuațiile vector-matrice:

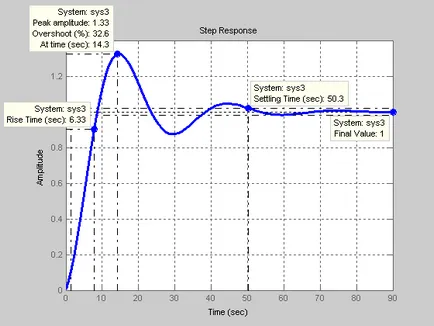
Figura 17 - Etapa PAC răspuns cu PID

Când au fost preparate exact modelul isolzovanii „input-output“ și modele „input-stare-ieșire“ același răspuns tranzitoriu (figurile 7 și 17), prin urmare, modelul „input-stare-ieșire“ pentru AAR cu PID calculat corect.

schema structurală PAC PID

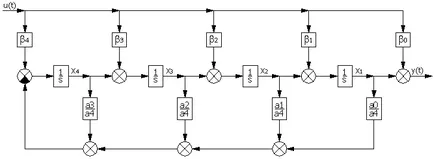
Figura 18 - Schema bloc a SAR cu PID

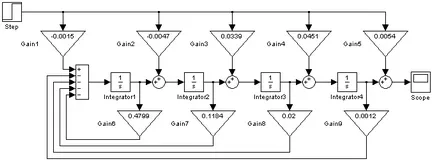
Figura 19 - Diagrama modelelor s-PAC cu PID

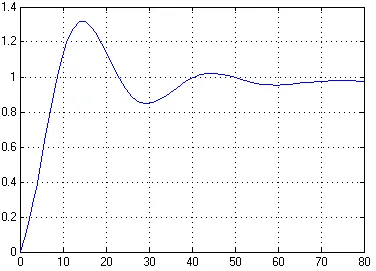
Figura 20 - Etapa PAC răspuns cu PID

răspuns tranzitoriu primit pe e-model, SAR cu Controlorul PID folosind pachetul sistem Simulink Matlab coincide cu caracteristicile tranzitorii obținute anterior, apoi s-model este construit, dreapta.

Evaluarea PAC cu PID maniabilitate

Evaluarea manipulare PAC va fi realizată cu ajutorul criteriului controlabilitate Kalman. matrice controlabilitate are forma (15):