Sistemul plan Arbitrare al forțelor - studopediya
Sub orice sistem de forțe înțelege totalitatea forțelor situate în același plan, linia de acțiune care nu se intersectează la un moment dat. Sistemul plan Arbitrare al forțelor poate fi mult simplificată prin aducerea de putere la un sistem de operare pentru a aduce centrul unui rezultat în centrul de forță este aplicată. numit vectorul principal și corpul ca un întreg va fi atașat la o pereche de forțe MO moment. numit principalul punct în raport cu centrul.
Principalul vector este egal cu suma geometrică a forțelor care aparțin sistemului, iar punctul principal MO - suma algebrică a momentelor de forțe pentru aducerea centrului, inclusiv suma algebrică a momentelor de cupluri de forță:
Valoarea numerică a vectorului rezultant este definit prin proeminențele sale pe axele:
Sensul vectorului rezultant este găsit prin direcționarea cosinusului unghiurilor:
în cazul în care. - versorii axelor Ox și Oy.
Termenii corp echilibru sub acțiunea unui sistem plan arbitrar de forțe sunt egale cu zero și vectorul rezultant în raport cu principalele puncte ale oricărui centru O:
Aceste condiții sunt îndeplinite dacă
Ecuațiile (1) sunt numite ecuațiile fundamentale ale echilibrului. Există alte două forme de ecuațiile de echilibru:
Sistemul de ecuații (2) axa x trebuie să fie perpendiculară pe linia care trece prin centrele A și B, precum și punctele A, B și C în sistem (3) nu se află pe o linie.
Exemplul C1. (. Figura C1) ADSV cadru rigid este fixat la punctul A suport de articulație și la punctul B - pivot mobil rulment pe role. Toate sarcinile și dimensiunile aplicabile sunt prezentate în figură.
Aceasta este dată de: F = 25 kN, a = 60 °, R = 18 kN, g = 75 °, M = 50 kN x m, b = 30 °, a = 0,5 m Definire :. Reacție la punctele A și B, cauzate de sarcină.
Decizie. 1. Se consideră echilibrul cadrului. Desenați axe xy și să tragă care acționează asupra cadrului de putere: forță. un cuplu forță la un cuplu M, un cablu de tensionare (modulo T = P) și leagă reacția. . (Reacția A lagăr pivot fix descrie două dintre elementele sale constitutive, rolele de susținere balama reacție este perpendiculară pe planul de referință).
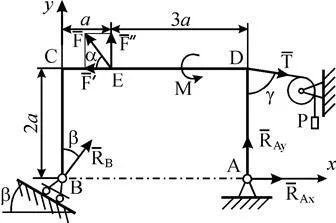
2. Pentru forma plană obținută sistemul cu trei forță de ecuații de echilibru. În calculul momentului de forță în jurul punctului Avospolzuemsya Pierre Varignon teorema, t. E. Extindeți forța în componente. () Și să ia în considerare faptul că. obținem:
Din ecuația (6) găsim:
Marks indică faptul că reacția și prezentată în orientate opus figură.
Pentru a verifica corectitudinea rezultatelor și să decidă să elaboreze o ecuație de verificare de echilibru sub forma momentelor tuturor forțelor cu privire la punctul C.
Exemplul C2. Design-ul este alcătuit dintr-o tijă gon AEC SK rigid și că, la punctul C (Fig. C2a), conectate între ele printr-o articulație cilindrică.
Conexiuni externe sunt la punctul A - balama fixă de suport, la punctul B - BB rod imponderabilă ¢, la punctul D - suport pivotant-mobil. Pentru a proiecta este aplicată forța. o pereche de forțe cu momentul M și distribuite uniform în zona HF q intensitatea sarcinii.
Aceasta este dată de: F = 10 kN, a = 60 °, q = 20 kN / m, M = 50 kN x m, a = 0,5 m.
Se determină reacțiile de constrângere la punctele A, B, C și D, datorită unei sarcini prestabilite.
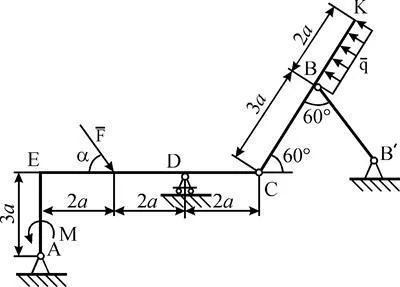
Decizie. 1. Pentru a determina sistemul de reacție dezmembrată printr-o balama C și ia în considerare primul arbore de echilibru CS (Fig. S2B). Desenați axe xy și trage acționează asupra forței tija: sarcină distribuită uniform înlocui forța. aplicat la porțiunea mijlocie a VC (numeric Q = q × 2a = 20 kN), tija de reacție BB ¢ direcționată de-a lungul tijei, iar acțiunea casate gon AEC reprezintă componente și reacția balama C.
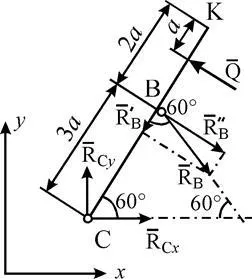
Pentru a obține un sistem de forțe plat este de trei ecuații de echilibru:
În calculul momentului forței se descompune în componente și utilizarea și Pierre Varignon teorema (.).
Din ecuația (9) găsim
2. Acum, ia în considerare soldul poligonului (fig. C2b).
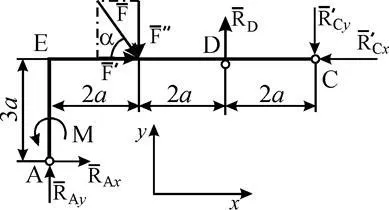
Act pe ea: forța. cuplu de forțe cu momentul M, reacția suportului D-pivotabil mobile, componente și reacție de susținere fixă A și pivotabil componentele și reacțiile. îndreptate opus față de reacțiile respective și. care au fost atașate la tija COP. Atunci când deciziile țin cont de faptul că numeric = i =. având în vedere egalitatea de acțiune și de reacție. Pentru acest sistem de forțe plat, de asemenea, suntem trei ecuații de echilibru:
În ecuația (12) pentru calcularea unui moment de forță. acesta din urmă defalcate în componente și teorema (ii) și aplicată Varignon lui.
Din ecuația (12) găsim:
Din ecuația (10):
Din ecuația (11):