Șapte modalități de a găsi aria unui triunghi

Și astfel, astăzi, considerăm că aceasta este o formă geometrică remarcabilă, ca un triunghi. Mai multe detalii despre găsirea aria unui triunghi.

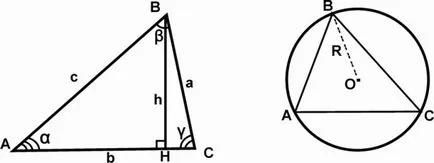
Am identificat șapte moduri principale de a găsi zona de triunghi. Să le considerăm mai detaliat.

1. Dacă ni se dă nici o parte a triunghiului și altitudinea atras de această parte, atunci vom înlocui pur și simplu aceste valori în formula.
2. Dacă avem lungimea a două laturi ale unui triunghi, iar unghiul dintre ele, atunci vom folosi formula.
3. Și dacă sarcina dată toate cele trei laturi ale triunghiului. este de a găsi o zonă avem nevoie de o formulă de Heron. în cazul în care - semiperimetrul.
4. Există o astfel de formulă, care are legătură cu zona unui triunghi, unde razele cercurilor inscriptionate si figurii. Dar cele mai importante nu ne interesează, pentru că trebuie să existe trei laturi ale triunghiului, iar în cazul în care acestea sunt, atunci suprafața triunghiului poate fi găsit pe formula lui Heron, atunci nu avem nevoie de nici raze (acestea sunt utilizate în cazurile în care este necesar pentru a găsi okruznosti rază ). Dar dacă avem doar unghiurile și raza cercului, atunci vom fi mare formulă. pe care le puteți identifica cu ușurință și părțile laterale ale triunghiului, și apoi găsi zona sa.
5. Un caz interesant, atunci când avem doar coordonatele vârfurile unui triunghi într-un plan. Aici, desigur, puteți găsi lungimea fiecărei laturi (sau valoarea unghiului) și apoi se calculează aria unui triunghi. Dar va fi mai ușor de opțiune, trebuie doar să scrie determinantul cele trei dimensiuni, în cazul în care fiecare rând din primele două elemente - coordonatele de un nod și a treia unitate. Apoi, jumătate din valoarea absolută a determinantului va fi zona triunghiului.
6. Nu mai puțin interesant este și cazul spațială aceeași problemă. Pentru a rezolva aceasta, trebuie mai întâi să găsească coordonatele celor două părți (vectori) ale triunghiului, care merg de la un nod. Și apoi, se calculează valoarea absolută a jumătate din produsul transversală a acestor părți.
7. În cele din urmă, ultimul caz este aceeași ca și cea anterioară, numai dacă au fost date coordonatele vectorilor, ei nu trebuie să caute. Pentru a calcula aria unui triunghi, care se află pe ele, trebuie doar să găsească jumătate din valoarea absolută a produsului vectorial.

Conținut legat de:

Împărtășește cu prietenii: