Proprietățile traiectorii de fază

1. Deciziile și definesc aceeași cale. Cu alte cuvinte, în timp soluțiile de schimbare nu modifică traiectoria de fază a sistemului (1).

2. Orice două sau faze traiectorii sunt disjuncte sau identice, adică traiectoria de fază nu se poate intersecta și două traiectorii diferite faze nu se pot intersecta.

3. Chiar dacă decizia de a crește t arbitrar aproape de punctul de repaus. punctul de imagine nu se poate ajunge la un punct în timp finit.

4. Dacă - soluție periodică (1), atunci ea corespunde unei traiectorii de fază închisă. (Fără auto-intersecții).

5. Fiecare cale de fază este fie

a) o linie unclosed fără auto-intersecții;

b) curba închise fără auto-intersecții;

Problema cea mai importantă în studiul sistemelor dinamice este acela de a identifica și studia staționar (starea de echilibru) mișcare.

De notat că termenul de mișcare pentru rezolvarea unui sistem de ecuații (1) este derivat din mecanica si pe scara larga.

a) Cel mai important tip de mișcări staționare - o stare de echilibru, care sunt determinate de sistemul final al ecuațiilor obținute din sistemul (1), atunci când derivatul este zero.

Sistemul de ecuații (7) are un număr de soluții m.

Prin urmare, sistemul (1) are o soluție.

Subliniem că relația (9) deține pentru t modificările de la zero la infinit. Să acorde o atenție la unele dificultăți terminologică, soluția (9) se numește mișcări staționare, deși se potrivește cu punctul de cale-la-, care este, desigur, rămâne staționară.

b) A doua clasă importantă a mișcării staționare într-un sistem dinamic sunt mișcare periodică, adică o astfel de circulație, în timpul căruia variabilele de stare oscileze cu perioada T:

După cum sa menționat traiectoria de mișcare periodică corespunzătoare este o curbă închisă în spațiul de fază.

Este necesar să se facă distincția între două tipuri fundamental diferite de mișcări periodice. Această limită cicluri și mișcarea conservatoare.

Ciclul Limita este un traseu închis izolat. Într-un cartier suficient de mică de această cale nu există nici alte traiectorii închise. Toate traiectoriile din cartier sau „rana“ pe un ciclu limită, sau eliminate din ea. (Detalii privind această problemă va fi explicată mai târziu)

Un fenomen foarte important în domeniu - de auto-oscilație. Auto-oscilații corespund spațiului fazei stabile (conceptul de durabilitate va fi explicată mai târziu) cicluri limită.

mișcarea conservatoare în sistemele tehnice se găsesc numai foarte rar.

c) Al treilea tip de mișcări staționare quasi-periodice sunt mișcări. Ele sunt numite mișcări non-periodice restricționate. Acest tip de mișcări de echilibru este foarte rar în sistemele tehnice.

· Să ne întoarcem la problema de a studia proprietățile soluțiilor staționare.

Stabilitatea poziției de echilibru.

Noi introducem conceptul de poziție de echilibru stabilitate Lyapunov. Mai întâi descriem ideea, atunci vom da declarația.

Poziția de echilibru se numește Lyapunov stabil dacă satisface condiția următoare. Lăsați condițiile inițiale ale soluțiilor ale sistemului (1) este suficient de aproape de poziția de echilibru. În acest caz, decizia sistemului va rămâne aproape de punctul de echilibru pentru orice t> 0.

limba # 949 - # 948; este formulată după cum urmează.

Să - poziția de echilibru.

Starea de echilibru se numește Lyapunov stabil dacă pentru orice număr dat pozitiv (arbitrar mic) # 949; Puteți găsi un număr pozitiv # 948; (# 949;), că în cazul în care inegalitățile:

pentru tot timpul infinit interval inegalitățile:

Starea de echilibru se numește asimptotic Liapunov stabil în cazul în care, în plus față de relațiile (11), (12) deține condiția:

Dacă există o # 949;, că cel puțin într-un caz nu se poate găsi un număr # 948; (# 949;), astfel încât atunci când inegalitatea (11) inegalitatea (12) pentru toate t> 0 poziția apoi de echilibru „și“, a declarat a fi instabile în sens Lyapunov.

Subliniem circumstanță importantă. Stabilitatea poziției de echilibru a sistemului în nici un fel nu ar trebui să fie o rezistență la balanța altor dispoziții. De exemplu, să presupunem poziția de echilibru a sistemului (1) va fi. Este posibil ca acesta este stabil și nu stabil. Sau nu este stabilă, și stabilă.

Exemplifice sensul definiției stabilității în conformitate cu Lyapunov poziției de echilibru.

Spatiul de fază este unidimensional - o linie dreaptă. Punctul de echilibru x = 0 este asimptotic stabil, deoarece, pentru orice funcție valoare x0 x (t) tinde la zero odată cu creșterea t.

Decizie. punct de echilibru este instabil, deoarece pentru orice valoare funcție de x0 este îndepărtată de la x = 0.

Acest sistem îndeplinește ecuația de îngrijire conservatoare:

Decizia lui. unde A și B # 958; - constante de integrare. Spatiul este faza bidimensional - plan.

Mai jos se va arăta că în această problemă toate traiectoriile de stat sunt familia infinit imbricată de cercuri centrate la origine.

întotdeauna dat # 949; puteți alege # 948; astfel încât cercul avea o rază mai mică # 949;. Echilibrul poziționează x1 = 0, x2 = 0 Lyapunov stabil, dar nu asimptotic stabil.

· Rezistența mișcări periodice.

Determinarea privind conceptul de stabilitate Lyapunov pentru următoarele mișcări periodice. Presupunem că este o soluție periodică (1). Soluție periodică numită Lyapunov stabilă dacă pentru fiecare predeterminat număr pozitiv # 949; Puteți găsi un număr pozitiv # 948; (# 949;), din cauza inegalității

Rezultă că pentru orice t> t0 inegalitatea

În cazul în care, în plus, condiția

Moțiunea periodică este asimptotic stabil în sens Lyapunov.

Conceptul de stabilitate prin Lyapunov poziției de echilibru foarte des folosit în știință și tehnologie. Odată cu mișcarea periodică a situației este mai complicată. În acest caz, restricțiile impuse de starea de stabilitate Liapunov sunt prea dure și rareori efectuate. Prin urmare, se folosește o condiție mai slabă stabilitate numita stabilitate orbitala a mișcărilor periodice.

mișcare periodică se numește orbital stabilă dacă pentru orice # 949; putem găsi # 948, (# 949;), astfel încât orice traiectorie de fază care, atunci când t = t0 stocat în # 948; traiectoria -neighborhood a mișcării periodice, nu va funcționa pentru toate t de la t0 la infinit de # 949; traiectoria -neighborhood a mișcării periodice.

Moțiunea periodică se numește orbital asimptotic stabil dacă toate calea declarat la t → ∞ se apropie asimptotic traiectoria mișcării periodice.

Noi explicăm conceptul de cartier pentru traiectoria. Pentru aceasta ne întoarcem la Figura 1, este prezentată o porțiune dintr-un traseu închis.

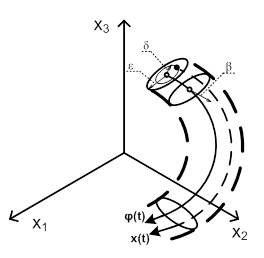
dedesubt # 949; - sau # 948; calea -neighborhood a însemnat un cilindru curbat care este construit după cum urmează. Traiectoria va fi considerat ca un fir subțire. Ia-un cerc de rază # 949; sau # 948; cu o gaură la centru. Acest cerc este pus pe calea, astfel încât să treacă prin centrul cercului. Apoi, cercul se deplasează de-a lungul unui traseu. În cursul gamei sale de circulație ar trebui să fie perpendicular pe planul tangent la traiectoria. Suprafața, care atrage în spațiul circumferința unui cerc, limita curbată este un cilindru sau o „gogoasa“. Vă reamintim că drumul este închis.

Stabilitatea Orbital necesită proximitate nu soluții reprezentative puncte și la acestea aproape la t = t0 soluții (t) și apropierea căii de puncte în spațiu, care, desigur, condiție considerabil mai slabă. Din stabilitatea cunoscută ar trebui să-l stabilitatea Lyapunov a orbitei mișcării periodice, dar nu și invers. De la stabilitatea orbital nu ar trebui să Lyapunov stabilitatea mișcării periodice.

· Metode de determinare a stabilității poziției de echilibru.

Prima metodă: determinarea stabilității poziției de echilibru a ecuației de primă aproximație. Această ecuație, urmând tradiția acceptată în domeniu va fi numită ecuația liniarizat.

Cea de a doua metodă (adesea numită metoda directă Lyapunov) se reduce la construirea unor funcții, care sunt numite funcții Lyapunov.

1) Criteriile de evaluare a stabilității în poziția de echilibru mic al sistemului liniarizat (1).

Sarcina de a investiga stabilitatea poziției de echilibru a sistemului (1) este posibil, folosind o schimbare de variabile, reduce problema stabilității poziției de echilibru la origine.

Prin urmare, sistemul inițial

convertit în

Sistemul (20) are o poziție de echilibru. și sistemul (21), - originea.

Așa cum se obișnuiește în literatura de specialitate, înlocuim în scrisoarea primită de sistem z cu litera x și plasați steaua funcției. adică, vom scrie sistemul de ecuații diferențiale, formal aceeași formă ca și (20), cu toate că, în esență, litera F în original și noile sisteme sunt marcate cu diferite funcții. (Modificat depinde). Reclasificarea descris mai sus variabile, în cazul în care a avut loc în memorie, nu va duce la erori.