polinomul zhegalkin
Zhegalkin polinom - polinom peste inelul $ \ mathbb_2 $, adică un polinom cu coeficienți de forma 0 și 1, în cazul în care produsul este luat ca o conjuncție, și ca adaos - XOR. Polinomial a fost propusă în 1927 de către Ivan Zhegalkin ca un mijloc convenabil de a reprezenta funcții booleene. În literatura străină, reprezentarea sub forma unui Zhegalkin polinom numit de obicei forma normală algebrică.
Teorema Zhegalkin - afirmarea existenței și unicitatea reprezentării oricărei funcții booleene ca Zhegalkin polinom.
Zhegalkin polinom este suma modulo două lucrări de variabile non-inversat și constante
Formal Zhegalkin polinom poate fi scris ca
sau într-o mai formalizata ca:
$ P = a \ oplus \ bigoplus_1 \ leq i_1<\ldots
Exemple de polinoame Zhegalkin:
- $ P = B \ oplus AB; $
- $ P = X \ oplus YZ \ oplus ABX \ oplus ABDYZ; $
- $ P = 1 \ oplus A \ oplus ABD. $
Conform teoremei lui Post, că sistemul de funcții booleene este completă, este necesar ca exista
- Cel puțin o funcție, nu salvați $ 0 $;
- Cel puțin o funcție, nu salvați $ 1 $;
- cel puțin o funcție neliniară;
- cel puțin o funcție non-monotonă;
- Cel puțin o funcție nesamodvoystvennaya.
Pe baza acestui fapt, sistemul de funcții $ \ bigl \ Langle \ pană, \ oplus, 1 \ bigr \ rangle $ este completă:
Pe baza acestui sistem și polinoame Zhegalkin construit.
Existența și unicitatea reprezentării
Teorema Zhegalkin: Fiecare funcție booleană poate fi reprezentat în mod unic ca Zhegalkin polinom.
Rețineți că diferite funcții booleene de $ n variabile $ $ ^ 2 $ bucăți. În acest tip de conjuncțiilor $ X_ \ ldots X_ $ sunt exact $ 2 ^ n $, din cauza $ n $ posibili factori sau fiecare parte a conjunctie sau nu. În polinomul în fiecare astfel de conjuncții costa $ 0 $ sau $ 1 $, adică, există $ 2 ^ $ Zhegalkin diferite polinoame de $ n $ variabile.
Acum este suficient pentru a dovedi că diferitele polinoame implementa diverse funcții. Să presupunem contrariul. Apoi, echivalând două polinomial diferite și se deplasează unul dintre ei la cealaltă parte a ecuației, obținem polinomul identic zero, și având coeficienți nenuli. Apoi, ia în considerare termenul cu un singur coeficient de cea mai mică lungime, care este, cu cel mai mic număr de variabile implicate în ea. Substituind unitate la locul acestor variabile, și zerouri în locurile rămase, constatăm că acest set este doar un termen are o singură valoare care este zero, pe una dintre seturile este setat la 1, o contradicție. Prin urmare, orice funcție booleană implementată de un Zhegalkin polinom unic.
Clădire Zhegalkin polinomul
Există mai multe moduri de a construi Zhegalkin polinom.
Conform tabelului de adevăr
Fie funcția f $ (x_1, x_2, \ puncte, x_n) $ este dat un tabel de adevăr. Scriem această primă funcție ca Zhegalkin polinom cu coeficienți nedeterminate. Apoi, unul câte unul substitut tot felul de seturi, în scopul de a crește numărul de unități și de a găsi coeficienții având în vedere faptul că $ a \ oplus 1 = \ bar $, si $ un \ oplus 0 = a $. Pentru fiecare permutare vom găsi doar un singur coeficient.
Exemplu: având în vedere o funcție $ f (x_1, x_2, x_3, x_4) $ și tabelul de adevăr:
Construim pentru ea un Zhegalkin polinom:
$ F (x_1, x_2, x_3, x_4) = a_ \ oplus a_ x_1 \ oplus a_ x_2 \ oplus a_ x_3 \ oplus a_ x_4 \ oplus a_ x_1 x_2 \ oplus a_ x_1 x_3 \ oplus a_ x_1 x_4 \ oplus \\ \ oplus a_ x_2 x_3 \ oplus a_ x_2 x_4 \ oplus a_ x_3 x_4 \ oplus a_ x_1 x_2 x_3 \ oplus a_ x_1 x_2 x_4 \ oplus \\ \ oplus a_ x_1 x_3 x_4 \ oplus a_ x_2 x_3 x_4 \ oplus a_ x_1 x_2 x_3 x_4 $
Deoarece $ f (0,0,0,0) = 0 $, atunci $ a_ = 0 $.
În continuare, vom înlocui toate celelalte seturi în ordinea numărului de unități ascendent, înlocuind valorile nou obținute în următoarea formulă:
$ F (1,0,0,0) = a_ \ oplus a_ = 1 \ rightarrow a_ = $ 1
$ F (0,1,0,0) = a_ \ oplus a_ = 0 \ rightarrow a_ = 0 $
$ F (0,0,1,0) = a_ \ oplus a_ = 0 \ rightarrow a_ = 0 $
$ F (0,0,0,1) = a_ \ oplus a_ = 0 \ rightarrow a_ = 0 $
$ F (1,1,0,0) = a_ \ oplus a_ \ oplus a_ \ oplus a_ = 1 \ rightarrow a_ = 0 $
$ F (1,0,1,0) = a_ \ oplus a_ \ oplus a_ \ oplus a_ = 0 \ rightarrow a_ = $ 1
$ F (1,0,0,1) = a_ \ oplus a_ \ oplus a_ \ oplus a_ = 0 \ rightarrow a_ = $ 1
$ F (0,1,1,0) = a_ \ oplus a_ \ oplus a_ \ oplus a_ = 1 \ rightarrow a_ = $ 1
$ F (0,1,0,1) = a_ \ oplus a_ \ oplus a_ \ oplus a_ = 0 \ rightarrow a_ = 0 $
$ F (0,0,1,1) = a_ \ oplus a_ \ oplus a_ \ oplus a_ = 0 \ rightarrow a_ = 0 $
$ F (1,1,1,0) = a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ = 1 \ rightarrow a_ = 0 $
$ F (1,1,0,1) = a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ = 0 \ rightarrow a_ = 0 $
$ F (1,0,1,1) = a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ = 1 \ rightarrow a_ = 0 $
$ F (0,1,1,1) = a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ = 0 \ rightarrow a_ = 1 $
$ F (1,1,1,1) = a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus \\ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ \ oplus a_ = 0 \ rightarrow a_ = $ 1
Astfel, polinomul Zhegalkin arată astfel:
$ F (x_1, x_2, x_3, x_4) = x_1 \ oplus x_1 x_3 \ oplus x_1 x_4 \ oplus x_2 x_3 \ oplus x_2 x_3 x_4 \ oplus x_1 x_2 x_3 x_4 $
Transformarea formei normale disjunctivă
Această metodă se bazează pe faptul că $ X \ oplus 1 = \ bar $. Dacă funcția este definită ca DNP, este posibil să se îndepărteze mai întâi disjungerea, folosind regula De Morgan, și toate negare înlocui adăugarea unei modulo doi, și apoi deschideți parantezele în mod normal, ținând cont de faptul că un număr par de termeni egali este egal cu zero, și un număr impar de elemente identice este egal cu un astfel de sumand. Sau puteți înlocui disjungerea în felul următor: $ A \ cerule B = AB \ oplus A \ oplus B $ $ (1) $.
Dacă funcția este definită în PDNF, apoi, din moment ce pentru orice valoare a variabilelor de intrare în unitatea nu ocupă mai mult de un membru al expresiei, apoi pur și simplu înlocuiți toate exclusive sau disjunctia.
Exemplu: Funcția Dan în DNF $ f (x_1, x_2, x_3, x_4) = (x_1 \ teren x_2 \ teren \ Neg x_3 \ teren x_4) \ cerule (\ Neg x_1 \ teren \ Neg x_4) \ cerule (x_1 \ teren x_2) \ cerule x_2 $, construi Zhegalkin polinom.
Noi scriem funcția ca aceasta:
$ F (x_1, x_2, x_3, x_4) = x_1 x_2 \ Neg x_3 x_4 + \ Neg x_1 \ Neg x_4 + x_1 x_2 + x_2 $;
Grupul de transformare termeni și utilizarea (1):
$ F (x_1, x_2, x_3, x_4) = (x_1 x_2 \ Neg x_3 x_4 \ oplus \ Neg x_1 \ Neg x_4 \ oplus x_1 x_2 \ Neg x_3 x_4 \ Neg x_1 \ Neg x_4) + (x_1 x_2 \ oplus x_2 \ oplus \ oplus x_1 x_2 x_2) $
Noi folosim proprietatile conjunctie $ A \ teren A = A $ și $ \ Neg A \ teren A = 0 $, iar $ A \ oplus A = 0 $, și va simplifica expresia:
$ F (x_1, x_2, x_3, x_4) = (x_1 x_2 \ Neg x_3 x_4 \ oplus \ Neg x_1 \ Neg x_4) + x_2 $
Din nou, folosim transformarea (1):
$ F (x_1, x_2, x_3, x_4) = x_1 x_2 \ Neg x_3 x_4 \ oplus \ Neg x_1 \ Neg x_4 \ oplus x_2 \ oplus (x_1 x_2 \ Neg x_3 x_4 \ oplus \ Neg x_1 \ Neg x_4) x_2 $
Să ne suport deschis pe reguli algebrice:
$ F (x_1, x_2, x_3, x_4) = x_1 x_2 \ Neg x_3 x_4 \ oplus \ Neg x_1 \ Neg x_4 \ oplus x_2 \ oplus x_1 x_2 x_2 \ Neg x_3 x_4 \ oplus \ Neg x_1 x_2 \ Neg x_4 $
Din nou, utilizați proprietățile conjuncție și XOR:
$ F (x_1, x_2, x_3, x_4) = \ Neg x_1 \ Neg x_4 \ oplus x_2 \ oplus \ Neg x_1 x_2 \ Neg x_4 $
Înlocuiți refuzul la adăugarea de $ 1 $:
$ F (x_1, x_2, x_3, x_4) = (x_1 \ oplus 1) (x_4 \ oplus 1) \ oplus x_2 \ oplus (x_1 \ oplus 1) x_2 (x_4 \ oplus 1) $
$ F (x_1, x_2, x_3, x_4) = x_1 x_4 \ oplus x_1 \ oplus x_4 \ oplus 1 \ oplus x_2 \ oplus x_1 x_2 x_4 \ oplus x_1 x_2 \ oplus x_2 x_4 \ oplus x_2 $
Aruncați termenii pereche și obține formula finală:
$ F (x_1, x_2, x_3, x_4) = x_1 x_2 x_4 \ oplus x_1 x_2 \ oplus x_1 x_4 \ oplus x_2 x_4 \ oplus x_1 \ oplus x_4 \ oplus $ 1
metoda de triunghi
Triangle Metoda codifică tabelul de adevăr în Zhegalkin polinom prin construirea unui tabel de sprijin triunghiular, în conformitate cu următoarele reguli:
- Construiți un tabel complet de adevăr, în care rândurile sunt în ordinea crescătoare a codurilor binare de la $ 000 de \ dots00 111 $ la \ $ dots11 $.
- Construirea matrice triunghiular auxiliar, în care prima coloană aceeași ca și coloana din valorile din tabelul de adevăr.
- Celula în fiecare coloană ulterioară se obține prin modulo 2 adăugarea a două celule ale coloanei anterioare - cu care se confruntă în același rând și rândul de jos.
- Coloane tabel auxiliar codurile binare sunt numerotate în același mod ca și rândurile din tabelul de adevăr.
- Fiecare cod binar este asociat cu unul dintre membrii polinomului Zhegalkin în funcție de poziția codului în care unitățile sunt. De exemplu, celula 111 $ $ $ corespunde unui membru al $ ABC, aprovizionată $ 101 $ - membru $ AC $, celulă $ 010 $ - $ pat și $ Dick, caseta $ 000 $ - $ 1 membru $, etc.
- Dacă linia superioară a unei coloane este una, termenul corespunzător este prezent în polinomial Zhegalkin.
De fapt, această metodă este o modificare a metodei de construcție în conformitate cu tabelul de adevăr așa cum este descris mai sus. Prin comparație, este mai convenabil ca calculele ocupă puțin spațiu și sunt mai greu de a face o greșeală, dar metoda triunghi necesită un număr mai mare de operații.
tabelul de conversie EXEMPLU adevăr în Zhegalkin funcție polinomială de trei variabile $ P (A, B, C) $ prezentate în Fig.
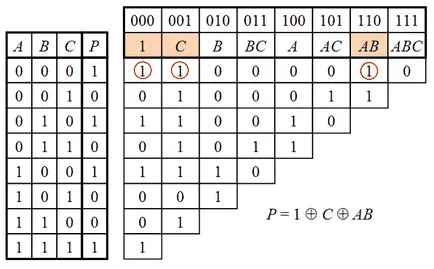
Pentru a obține o formulă este utilizată pentru a calcula orice caz, este necesar din celula în care este înregistrată, să meargă în toate modurile posibile la stânga, la $ coloana „“ P „“ masa de $ adevăr, ceea ce se mută spre stânga și spre stânga și în jos, notați valorile din celulele se încheie și le-a pus toate între ele modulo 2.
Astfel, în prima coloană a înregistrat top coeficient $ a_0 = P (0,0,0) $,
În al doilea rând - $ a_1 = P (0,0,0) \ oplus P (0,0,1) $,
în al treilea - $ a_2 = P (0,0,0) \ oplus P (0,0,1) \ oplus P (0,0,1) \ oplus P (0,1,0) = P (0,0 , 0) \ oplus P (0,1,0) $,
$ A_3 = P (0,0,0) \ oplus P (0,0,1) \ oplus P (0,0,1) \ oplus P (0,0,1) \ oplus P (0,1,0 ) \ oplus P (0,1,0) \ oplus P (0,1,0) \ oplus P (0,1,1) = \\ = P (0,0,0) \ oplus P (0,1 , 0) \ oplus P (0,1,0) \ oplus P (0,1,1), $
și așa mai departe, adică, construcția coeficienților polinomiale din tabel auxiliar sunt calculate automat.
transformarea Möbius
Având în vedere o funcție booleană $ f: B ^ n \ rightarrow B, \; \; B =<0; 1>$. Orice funcție booleană poate fi reprezentat ca un Zhegalkin polinom, într-un mod unic.
Să $ i = (i_1, I_2 i_n.), \; \; i_k \ în $, și să introducă notația $ x ^ \ sim \ stânga [\ începe x, \; \; i_k = 1 ianuarie \; \; i_k = 0 \ end \ dreapta. $
Apoi Zhegalkin polinom poate fi scris ca: $ f (x) = \ bigoplus \ limits_i \ alpha_i \ cdot x_1 ^ \ cdot x_2 ^ \ cdot $$ \ dots $$ \ cdot x_n ^ $, unde $ \ alpha_i \ în <0; 1>$.
$$ set de coeficienți poate fi privit ca o funcție de $ \ alpha $, pentru un anumit indice set $ i = (i_1, I_2, \ puncte i_n) $, adică $ \ alpha: i \ mapsto \ alpha_i $.
Evident, funcția $ f $ poate fi scris astfel: $ f (x) = \ bigoplus \ limits_i \ alpha_i \ cdot [x_1. \; $ Dacă $ \; \; i_1] \ cdot [x_2. \; $ Dacă $ \; \; I_2] \ cdot $$ \ puncte $$ \ cdot [x_n. \; $ Dacă $ \; \; i_n] $.
Aici $ record de [x_k. \; $ Dacă $ \; i_k] $ înseamnă elelement $ x_k $ prezentă în termenul corespunzător al polinomului dacă numai i_k $ = 1 $. În cazul în care pentru unele $ x $, $ i \ succ x $ *, atunci termenul va fi de cel puțin un factor egal cu zero, iar un astfel de termen pentru suma nu va fi afectată. Prin urmare, este clar că $ f (x) = \ bigoplus \ limits_ \ alpha_i $ $ (2) $ Gasim cartografiere $ f \ mapsto \ alpha $.
$ * $ $ I \ succ x $ înseamnă că $ x $ "mai puțin" $ i $ ca o secvență de biți
Teorema: Fie o functie $ f $. Apoi, funcția $ \ $ alpha_x pot fi găsite de formula: $ \ alpha_x = \ bigoplus \ limits_ f (j) $ (3)
Dovedim prin inducție cu privire la numărul de unități din vectorul $ x $ și, pentru a ne indica numărul de unități $ greutate (x) $.
1) de bază: dacă $ x = 0 $, atunci, evident, $ f (0) = \ alpha_0 $
2) Fie teorema este adevărată pentru toate în greutate cantități $ (x) Luați în considerare suma de $ \ stânga [\ bigoplus \ limits_ \ bigoplus \ limits_ f (j) \ dreapta] $. Fiecare element $ f (j) $ este conținută în ea, numai dacă $ j \ pRec x $, iar pentru $ j fix, x $ element de $ f (j) $ sunt exact cât de multe ori sunt $ i $. astfel încât $ j \ pRec i \ pRec x $. Este ușor de văzut că o astfel de $ i $ sunt exact 2 $ ^ -1 $, adică, un număr impar de ori. Apoi \ $ stânga [\ bigoplus \ limits_ \ bigoplus \ limits_ f (j) \ right] = \ bigoplus \ limits_ f (j) $. Dar apoi $ f (x) = \ stânga [\ bigoplus \ limits_ f (j) \ right] \ oplus \ alpha_x \ Leftrightarrow f (x) \ oplus \ bigoplus \ limits_ f (j) = \ alpha_x \ Leftrightarrow \ alpha_x = \ bigoplus \ limits_ f (j) $. Adică, atunci când $ wt (x) = k $ formulă deține de asemenea, atunci pentru orice $ x $ ruleaza $ \ alpha_x = \ bigoplus \ limits_ f (j) $. Mapping $ f \ rightarrow \ alpha $ este numit, de asemenea, o transformare Möbius. Se poate vedea că $ (2) $ și $ (3) $ - aceasta este aceeași conversie. Deci, dacă aplicăm transformarea Möbius la funcția, și apoi re-aplică aceeași transformare pentru a obține o funcție, apoi re-obține versiunea originală funcția $ f $. Aceasta este transformarea Möbius înapoi la sine, cu alte cuvinte, este o involuție. Clasa $ L $. Teorema pe zamknytosti clasa $ L $ Integrale improprii domeniului nemărginit Proprietățile integralelor dubleA se vedea, de asemenea: