Numărul de diferite k-subseturi de seturi-n elementare elementare - studopediya

Să vedem acum, așa cum există diferite subseturi de k elemente ale setului format din n elemente (k <п).

TeoremaChislo diferite subseturi k-n-element al setului este egal cu elementar

în cazul în care reducerea n! = N * (n - 1) *. * 3 * 1 * 2 factorial numit număr n (factorial n-citibil). Și 0! = 1. O reducere.

Dovada. Pentru a construi un subset element k al A, este necesară (k - 1) set -Element pentru a conecta unul dintre n - k + 1 elemente care nu sunt incluse în acest subgrup. Pe măsură ce numărul de (k - 1) subseturi -Element de aceeași, și fiecare dintre aceste subseturi poate fi-elementul k n - k + 1 moduri, regula de bază a combinatorie număr-Toriki obține * (n - k + 1) subseturi. Cu toate acestea, nu toate aceste subseturi sunt diferite, deoarece orice k este un subset elementar poate construi, de asemenea, moduri k. Prin urmare,

Deoarece - numărul de subseturi Singleton A - este egal cu n, atunci

Element k arbitrara subset A este o combinație sau probă, iar numărul - numărul de combinații sau combinații de n elemente de k elemente.

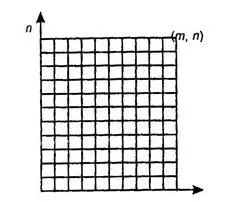
Coeficienții binom au o interesantă geometrică Interprom-tatsiyu. Să aibă o dimensiune dreptunghiulară tablă de șah m de n, timp-deplasări în planul de coordonate. Acest consiliu este format din m * n pătrate elementare separate de n - linia 1 hori-tal și m - 1 verticală. Se determină cât de multe diferite căi mai scurte se poate ajunge de la punctul (0, 0) la punctul (m. N) pe acest bord.

Fiecare cea mai scurtă cale lider din punctul (0, 0) până la punctul (m, n), în mod evident, este format din m + n laturi pătrate elementare, printre care m hori-zontally și n verticale. Aceste căi diferă doar 1 număr de laturi verticale și orizontale. Prin urmare, numărul total de căi egal cu numărul de moduri în care a m + n părți pot alege n-ver-local, adică, acest număr este.

Rețineți că nu a putut să conta pe laturile verticale,

precum și pe orizontală. Adică, există o varietate de cele mai scurte rute și, în consecință, egalitatea:

Această egalitate se numește „formulă de simetrie.“

Din această formulă, avem rezultatul:

având titlul „adăugarea de formula“. Dovedim acest efect.

Echipa de volei combinat Universitatea are 15 persoane. Cât de multe opțiuni diferite ar trebui să ia în considerare antrenorul înainte de joc să anunțe lista de jucători în joc?

Soluție: Numărul de jucători ai echipei de volei este de șase. Prin urmare, numărul de toate opțiunile posibile - un număr de diferite subseturi, format din șase elemente într-un set de cincisprezece elemente. Astfel, prin Teorema 2 avem