Notăm proiecții pe axele de coordonate, prin
Obținem - această formulă este vectorul principal și calcularea vectorului nazyvaetsyaRazlozhenie al vectorilor unitare axelor de coordonate. numerele
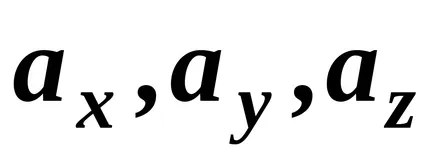
Proiecțiile vectorului pe axele de coordonate sunt numite coordonatele sale. Aceasta este semnificația lor geometrică.
Ecuația vector este uneori scris în formă simbolică
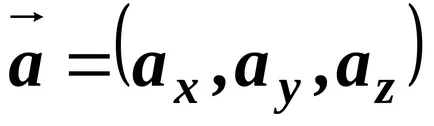
Cunoscând proiecția vectorului poate găsi cu ușurință lungimea sa, și anume, modul. Pe baza teoremei privind lungimea casetei în diagonală.
Ie vector unitate este rădăcina pătrată a sumei pătratelor proiecțiile pe axele. coordonate.
Lăsați unghiurile vectoriale cu axele de coordonate respectiv
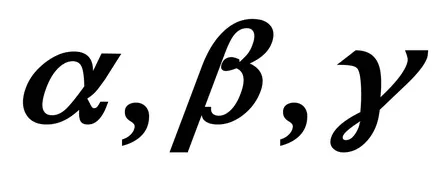
colțuri Opr.12Kosinusy care formează un vector de axele de coordonate, nazyvayutsyanapravlyayuschimi kosinusamivektora.
Dacă vectorul este dat în avion, atunci.
Ei au o proprietate remarcabilă:
.
Din formulele (*) implică faptul că coordonatele vectorului unitate sunt cosinusului direcție, adică .
5. Acțiuni asupra vectorilor în formă componente
Pentru orice punct din DSC coordonatele OM-radius-vector sunt coordonatele sale
Dacă la începutul vectorului nu coincide cu originea, dar coordonatele cunoscute ale Start A și punctul final B, coordonatele vectorului

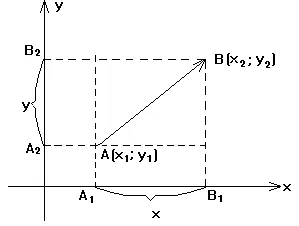
.
Acest spațiu bidimensional (R2).
În mod similar, în spațiul tridimensional. dacă
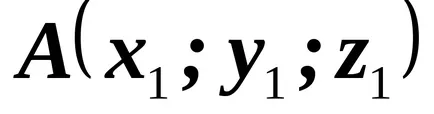
În cazul în care coordonatele cunoscute ale vectorului
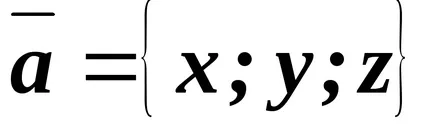
.
De cosinusului direcție ale fiecărui vector sunt calculate prin următoarele formule:
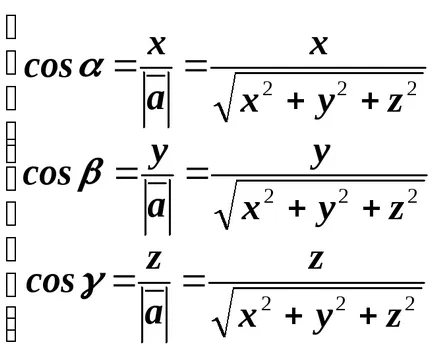
Dacă vectorii



Opusul este adevărat, și anume, în cazul în care relația,


§3. spațiu vectorial dimensional N. dependență liniară și independența vectorilor.
N - spațiu vectorial dimensional.
2. dependența lineară și independența vectorilor
3. Baza spațiului vectorial. Extinderea vectorului în baza
spațiu 1.N- vector dimensional
Să presupunem că avem un sistem

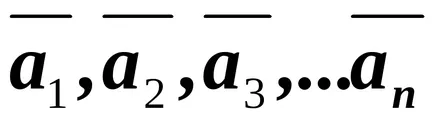
tip Opr.13 .Vyrazhenie :, (3.1) unde

vectori Opr.14.Sistema
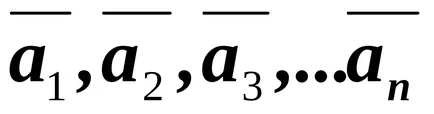

Dacă o combinație liniară (3.1) este egal cu zero, cu condiția ca cel puțin unul dintre numerele

Dacă sistemul conține mai mult de un vector
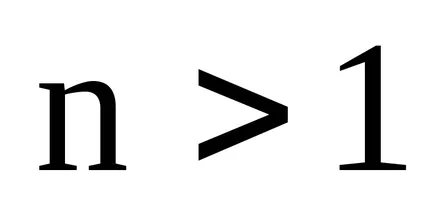

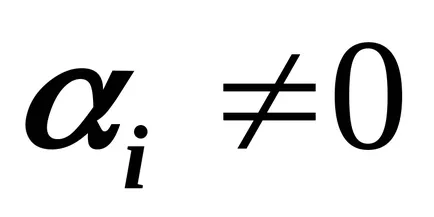


.
În cazul în care toți membrii (3.3) pentru a trece la o parte, constatăm că o combinație liniară este egală cu zero, cu condiția ca coeficientul vectorului
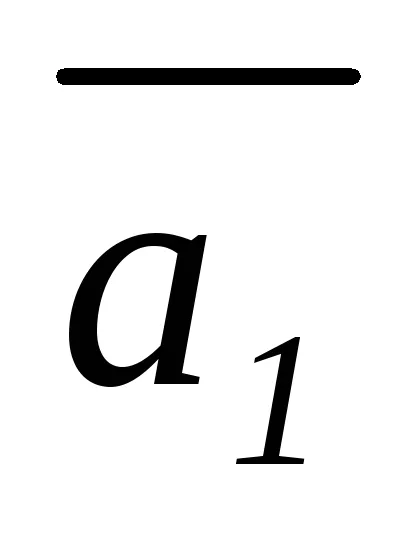
Vyvod.Esli cel puțin unul dintre vectorii este o combinație liniară (de exemplu, exprimat în termeni de celălalt), atunci întregul sistem de vectori este liniar dependent. Condițiile necesare și suficiente pentru dependența liniară a celor doi vectori pe un plan (în prostranstveR2) este coliniaritate lor, și în spațiul tridimensional (R3) - coplanarității lor.
Un sistem format dintr-un vector (R1 spațiu) este dependentă liniar, dacă vectorul este zero, iar dacă aceasta este diferită de zero - adică liniar independent.
În spațiul

În spațiul
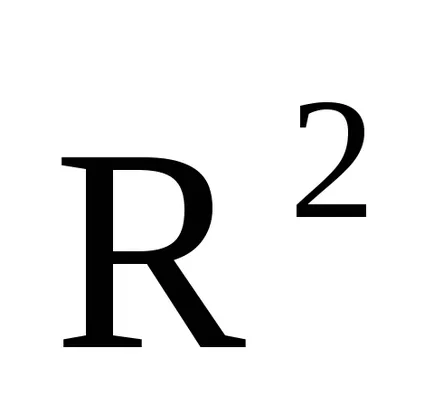
Dacă există un spațiu liniar

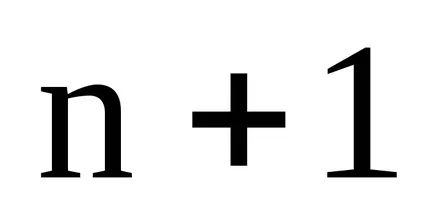
Numărul maxim posibil de vectori liniar independenți într-un spațiu finit-dimensional este dimensiunea acestui spațiu. În cazul în care dimensiunea spațiului este


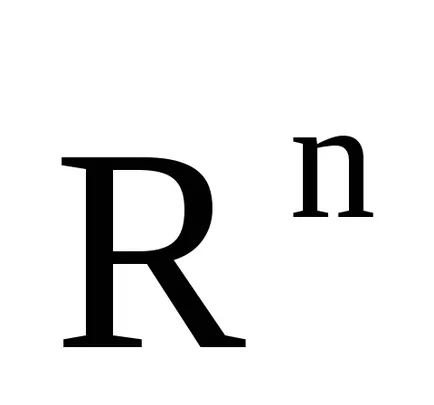
Opr.15.Sistema


Vectorii de bază pot fi descompuse în orice spațiu vectorial, cu un mod unic.
Descompună bază vector vectori - este să se prezinte ca o combinație liniară a vectorilor această bază.
În cazul în care baza este

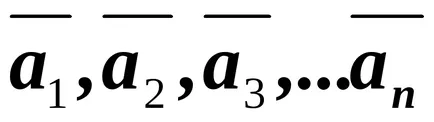

Coeficienții acestei extinderi, și anume, Număr nazyvayutsyakoordinatami vector
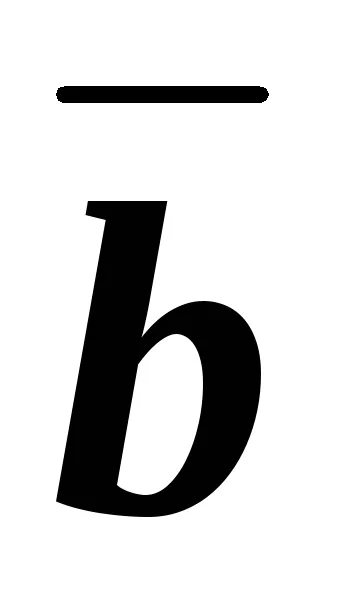
Pentru a găsi aceste numere trebuie să instituie un sistem de

Fiecare ecuație este compus cu formula (3-3) din coordonatele respective ale acestor vectori.
EXEMPLU EXEMPLU Având în vedere vectorii:
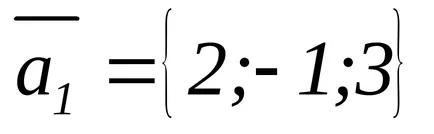
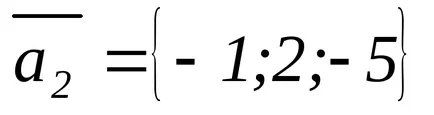

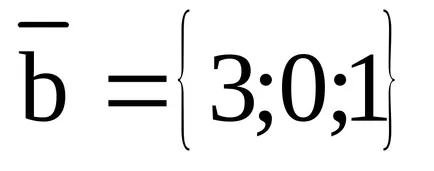
Arătați că vectorii
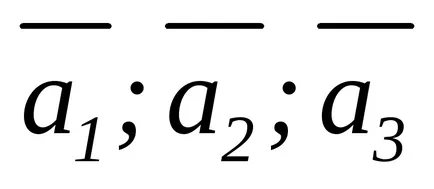

Decizie. vectori
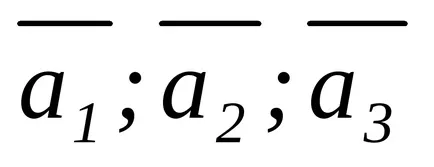
vector descompus

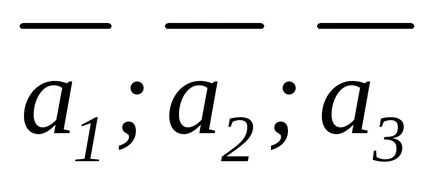
. (*)
Deoarece vectorul vectorilor de bază obținute prin formula (*), atunci fiecare dintre ei coordonate se obține din coordonatele corespunzătoare ale acestor vectori în aceeași formulă (*).