Moduri de mișcare fluidă

În funcție de tipul de lichid, viteza și natura pereții delimitatori fluxul, există două moduri de bază ale mișcării: a laminară și turbulentă. laminar numita ordonat mișcare atunci când straturile individuale aluneca unul peste altul, fără a se amesteca (Figura la).

regim de curgere laminara pot fi observate mai frecvent în fluide vâscoase, cum ar fi uleiul, vaselina, și așa mai departe. N.

Modul apel turbulent, în care mișcarea aleatorie se produce atunci când particulele de lichid se deplaseze de-a lungul unui traseu complex și straturile de fluid amestecat continuu unul cu celălalt (fig. B).

Existența a două regimuri de curgere a fluidului au fost observate în 1839 și Hagen în 1880 D. I. Mendeleevym.

Moduri suficient de completă studii de laborator de circulație și problema impactului lor asupra caracterului pierderii capului de viteză pentru prima dată, a studiat fizicianul englez Reynolds.

Instalarea studiului Reynolds a modurilor de mișcare fluid înainte de apariția unei sută în Fig. 27. Un vas este umplut cu lichidul de testat. Pentru nava A în partea inferioară a tubului de sticlă 1 este conectat cu robinet 2, care reglează debitul în tub. Și peste vasul este un vas B cu soluție de colorant. B se îndepărtează de tubul vasul 3 cu macaraua 4. Capătul tubului 3 este înfășurat în tubul de sticlă 1. Pentru a umple containerul 5 a este un tub cu un dispozitiv de blocare 6.

În mișcare de curgere laminară a fluidului în tubul 1 soluția colorantă trickle curge din tubul 3 are o vedere clară a filamentului de-a lungul lungimii tubului 1.

Deoarece deschiderea robinetul 2 este crescut, iar modul viteza de deplasare devine turbulentă, prelingerea devine caracterul ondulat, iar la viteze mai ridicate complet erodate și amestecat cu lichidul din tub. Odată cu închiderea treptată a robinetului, aceste fenomene au loc în ordine inversă, adică. E. turbulenta laminar înlocuit.

Experimentele au arătat că tranziția de la laminar la curgere turbulentă se produce la o anumită viteză (aceasta se numește viteza critică), care este diferit pentru diferite lichide și diametre de țeavă; în care critică viteza crește cu viscozitate fluid și cu scăderea țevilor cu diametru.

Reynolds și alți câțiva cercetători de au fost determinate empiric că semnul modului de conducere este un număr adimensional, care ia în considerare caracteristicile fluxului principal

în care - viteza, m / sec; R - raza hidraulică, m; v - cinematică viscozitate, m2 / sec.

Acest raport se numește numărul Reynolds. Valoarea Re, la care regimul turbulent devine laminar, numit critic numărul ReKp Reynolds.

Dacă valoarea reală a Re, calculat conform unei formule pentru a fi mai mare decât Re critică> ReKp - Mod de mișcare turbulentă când Re

Pentru debitul de presiune în tuburi cilindrice mai convenabil pentru a determina numărul Reynolds în raport cu diametrul d, t. E.

unde d - diametrul conductei.

În acest caz, se pare ReKp egal

2300. Dacă, în formula pentru conducte cu secțiune transversală circulară d exprimată în termenii razei hidraulice. atunci vom obține ReKp = 575. Pentru alte conducte și canale de secțiuni transversale necirculare poate lua valoarea numărului Reynolds critic ReKp = 300 (la calcularea razei hidraulice peste Re).

Căderea de presiune în flux laminar

Studiile arată că, cu flux laminar într-un tub circular este viteza maximă a axei țevii. În peretele țevii de viteză este zero, deoarece Particulele de fluid sunt acoperite cu suprafața interioară a conductei cu un pat fix subțire. Din pereții tubului pe axa sa de rapid crește lin. distribuția vitezei grafic pe secțiunea transversală a fluxului este un paraboloid de revoluție și un paraboloid axial secțiune plană - parabole pătratice (figura 4.3).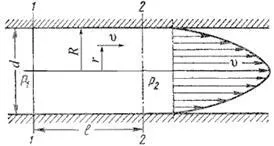

schema Figura pentru examinare flux laminar

Ecuația privind variabilele # 965; și r, este următoarea:

în care P1 și P2 - respectiv o presiune în secțiunile 1 și 2.

În r țeavă valoarea pereților = R. viteza medie # 965; = 0, și atunci când r = 0 (pe axa de curgere a) viteza de rotație este la maxim

Acum definesc curgerea fluidului în curgere laminară într-o conductă circulară. Deoarece diagrama de distribuție a vitezei într-un tub circular are forma unui paraboloid de rotație cu o valoare maximă a vitezei în conducta centrală, debitul este numeric egal cu volumul paraboloidului. Definim acest volum.

Viteza maximă dă înălțimea paraboloidului

După cum se cunoaște din geometria, volumul și aria de înălțime paraboloid h # 961; R2 este

și în cazul nostru

Dacă, în schimb R substituie diametrul țevii d, formula (4.4) ia forma

Debitul în conducta poate fi exprimată prin viteza medie:

Pentru a determina pierderea de presiune a fluidului în curgere laminară într-o conductă circulară de lungime l considerăm porțiunea de țeavă pe care curge fluxul în regim laminar (figura 4.3).

Pierderea de presiune conductă este egală cu

Dacă coeficientul de viscozitate dinamică de formula # 956; înlocuit prin viscozitatea cinematică # 965; și densitatea # 961; ( # 956; = # 965; # 961; ) Și împărțiți ambele părți de greutatea volumetrică a fluidului # 947; = # 961; g, obținem:

Deoarece partea stângă a acestei ecuații este egală cu presiunea pierderilor hpot într-un tub de diametru constant, în final, această ecuație ia forma:

Ecuația poate fi transformată într-o formulă universală Darcy-Weisbach, care este în cele din urmă scrisă ca:

unde # 955; - coeficientul de frecare hidraulic la care curgerea laminară se calculează prin expresia:

Cu toate acestea, în regim laminar pentru determinarea coeficientului de frecare hidraulică # 955; TM Basta recomandă Re <2300 применять формулу

Căderea de presiune pentru lichid flux turbulent

După cum sa arătat mai sus, caracteristica de curgere turbulentă de amestecare, viteza și presiunea fluidului pulsații. Atunci când se utilizează un dispozitiv deosebit de sensibil pentru a măsura pulsație-recorder, de exemplu, rata de timp, la un punct fix în fluxul, vom obține o imagine similară cu cea prezentată în figura 4.4. Viteza fluctuează în mod aleatoriu în jurul valorii de o valoare medie de-a lungul timpului # 965; OCP că acest caz rămâne constantă.

Caracter curent linie în țeavă la un moment dat este foarte variat (Fig.4.5).

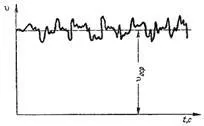
Figura. Viteza de pulsație într-o curgere turbulentă. Figura. Natura liniilor de curgere în fluxul turbulentă

Când regimul turbulent de curgere a fluidului în curba conductă de distribuție a vitezei are forma prezentată în figură, cu o grosime de strat limită subțire # 948; fluidul curge în mod laminară, în timp ce straturile rămase în regimul de curgere turbulentă și sunt numite miez turbulente. Astfel, strict vorbind, mișcarea turbulentă în formă pură nu există. Aceasta este însoțită de o mișcare laminară la pereți, deși stratul # 948; un regim laminar este foarte mic în comparație cu miezul turbulent.

Figura. Modelul de mișcare turbulentă a fluidului

Formula de bază pentru calculul pierderii capului în curgerea turbulentă a fluidului în conducte circulare este deja prezentată mai sus formulă empirică, numita formula Darcy-Weisbach și având următoarea formă:

Singura diferență este în valorile coeficientului de frecare hidraulică # 955;. Acest raport depinde de numărul Reynolds Re și factorul geometric adimensională - rugozitate relativă # 916; / d (sau # 916; / r0, unde r0 - raza tubului).

Pentru prima dată lucrarea cea mai cuprinzătoare cu privire la definirea au fost date II Nikuradse, care se bazează pe datele experimentale reprezentate grafic LG (1000 # 955;) de LG Re pentru mai multe valori ale # 916; / r 0. Experimentele Nikuradze au fost efectuate pe tuburi cu o rugozitate artificială predeterminată obținută prin atașarea granule de o anumită dimensiune la peretele interior al conductei. Rezultatele acestor studii sunt prezentate în Fig. 4.7, unde curbele în funcție lg (1000 # 955;) prin lg Re pentru un număr de valori # 916; / r0.

Modul Direct I corespunde mișcării fluidului laminar.

În plus, graficul poate fi considerat trei zone.

Prima zonă - zona de mici și Re # 916; / r0, unde coeficientul # 955; Aceasta nu depinde de rugozitatea, dar determinată numai de numărul Re (linia marcată pe figura II). Această zonă este hidraulic conducte netede. Dacă numărul Reynolds este în intervalul de 4,000

Pentru a determina există, de asemenea, formula empirică PK Konakova, care se aplică pentru tuburi hidraulice netede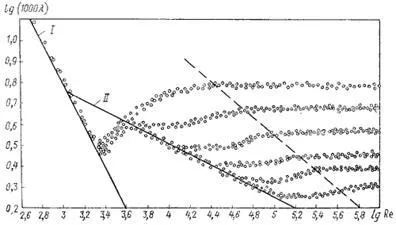

Figura. Program Nikuradze

În a doua regiune, situată între liniile II și o linie punctată spre dreapta, coeficientul # 955; simultan depinde de doi parametri - Re numărul și rugozitatea relativă # 916; / r0, care poate fi înlocuit cu # 916; e. Pentru a determina raportul # 955; în acest domeniu pot servi ca o formulă universală AD Altshul:

unde # 916; e - rugozitatea absolută echivalentă.

Valorile caracteristice # 916; e (în mm) pentru țevi din diferite materiale sunt prezentate mai jos:

A treia zonă - regiunea de înaltă Re și # 916; / r0, unde coeficientul # 955; Ea nu depinde de numărul Re, definit ca o rugozitate relativă (zona din dreapta liniei punctate). Această regiune țevi brute în care toate liniile cu diferite rugozități paralele. Această zonă se numește modul de auto-domeniu sau rezistența pătratică, deoarece aici pierderile hidraulice sunt proporționale cu pătratul vitezei.

definiție # 955; pentru această regiune produc Altshul cu formula simplificată:

sau formula Prandtl - Nikuradze:

Astfel, pierderea de presiune definită prin formula Darcy-Weisbach, poate fi determinată prin cunoașterea coeficientului de rezistență hidraulică, care este determinată în funcție de numărul Reynolds Re și rugozitatea absolută echivalentă # 916; e. Pentru comoditate, un rezumat al definiției # 955; sunt prezentate în tabel.

Utilizați date în tabel. 4.1 Formulele pentru determinarea ratei # 955; Nu este întotdeauna convenabil. Pentru a facilita calculul, puteți utiliza nomograma Colebrook-White (desen), prin intermediul căruia cunoscute și Re # 916; e / d este destul de simplu definit # 955;.

Tabel pentru determinarea coeficientului de frecare hidraulică

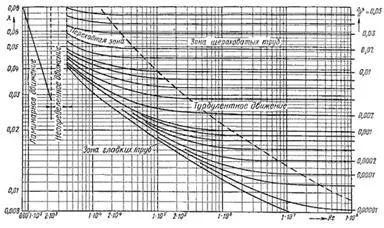
Figura. Colebrook-White nomogramă pentru determinarea coeficientului de frecare hidraulică

întrebări de testare pentru CPC:

legile de bază 1.Nazovite de mișcare a lichidelor în conducte

mișcare fluid 2.Rezhimy

3. Valoarea numărului Reynolds

4. Descrie configurarea Reynolds pentru investigarea moduri de mișcare fluidă