Metodele de conversie metoda de desenare pentru înlocuirea planele de proiecție ale metodelor de rotație metodice

De multe ori pentru conducere forme drepte, plane sau forma spațială în declarația de confidențialitate, care este necesară pentru a rezolva problema, este necesar să se înlocuiască cele două planuri de proiecție. Tranziția de la V / avioanele H ale unui anumit sistem la noul V1 / H1 poate fi realizată prin una dintre schemele prezentate mai jos:

Figura 12 este dat un punct A în sistemul de V / H. Apoi, trecerea de la sistemul V / H la sistemul V1 / H1. realizat noua axă de proiecție X1, a găsit o nouă proiecție a1 punctul A. Mai mult Sistem V1 / H este înlocuit cu un nou sistem de avioane de proiecție V1 / H1 - în locul planului orizontal de proiecție a introdus un nou H1 plan.

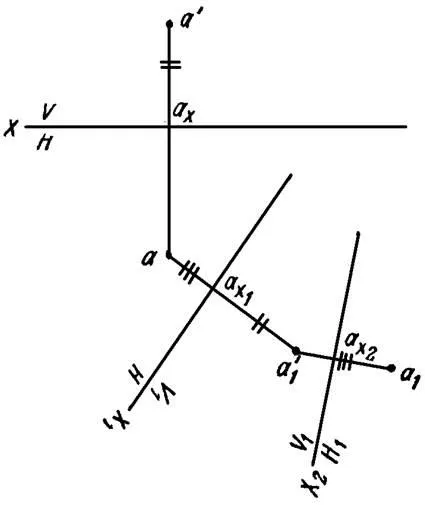
Poziția noilor axe ale proeminențelor este selectat în conformitate cu condițiile specifice ale problemei.

Exemplul 6. Pentru a determina adevarata forma unui triunghi ABC (Figura 13).

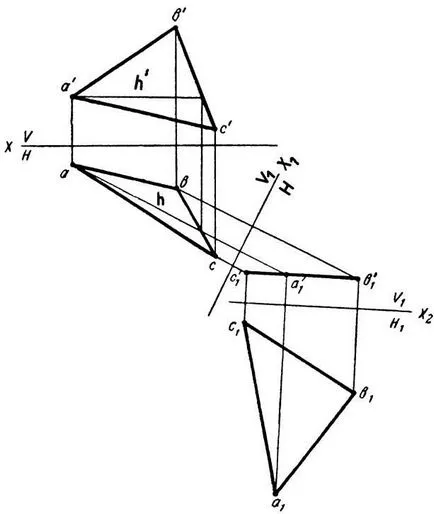
Triunghiul este proiectat pe un full-size pe orice plan de proiecție, în cazul în care el este o paralelă cu acest plan. Pentru triunghiul ABC transformat paralel cu unul dintre planurile de proiecție, trebuie să efectuați o avioane de substituție duble.

Vă rugăm să înlocuiți planul V la V1 plan. V1 perpendicular pe planul triunghiului ABC alege planul - o nouă proiecție axa X1 ar trebui să fie perpendiculară pe proiecția orizontală a unui h orizontal. Un nou cproektiruetcya proiecții plan frontal triunghi într-o linie dreaptă c'1 a'1 b'1. Apoi, vom introduce o nouă proiecție H1 plan paralel cu planul triunghiului.

Planul terenului a1 b1 c1 ABC triunghi în noul sistem - adevărata valoare a acesteia.

Primer7. SAVS dat piramidei (Figura 14). Se determină valoarea unghiului diedru la marginea AB.

Problema se reduce la construirea unghiului de proiecție pe planul de proiecție perpendicular pe marginea ei.

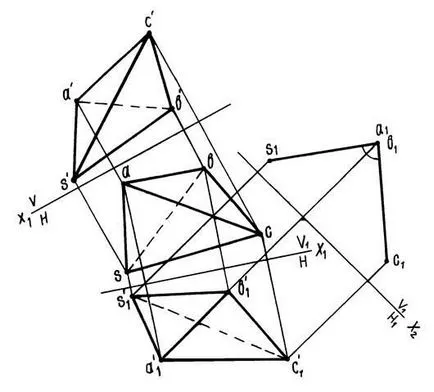
Deoarece marginea AB - situația generală drept, este necesar să se facă două înlocuirea succesivă a planului de proiecție. Planul V este înlocuit planul V1. paralel cu segmentul AB.

Am găsit o nouă proiecție frontală s'1 a'1 b'1 c'1 SAVS piramida pe un nou plan frontal proiecții. Apoi sistemul V1 / H pentru a trece sistemul V1 / H1. Plane H1 sunt aranjate perpendicular pe segmentul AB. Pe marginea plan H1 AB este proiectat pe un punct, iar fețele și SAV SAV - literalmente. Unghi s1 c1 a1 este dorit.

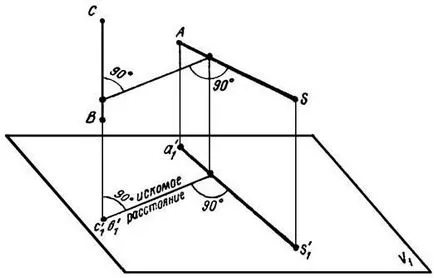
Primer8. SAVS dat piramidă (Figura 15). Se determină distanța cea mai scurtă dintre marginile SA si BC.

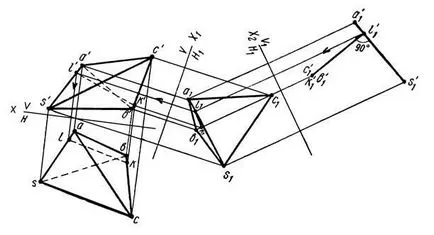
SA directe si BC sunt oblic. Prin urmare, problema se reduce la determinarea cea mai scurtă distanță între două linii oblice. Pentru a rezolva problema, este necesar să se facă o astfel de schimbare la planul de proiecție, la noul sistem al uneia dintre linii, cum ar fi soarele (Figura 16), sa dovedit a fi perpendicular pe un plan de proiecție. Înlocuirea planului de proiecție sunt efectuate V / H → V / H1 → V1 / H1.

În consecință, metodele de rezolvare a problemelor de conversie este de a pune în aplicare patru pași de bază:

1) transformarea directă într-un nivel generic direct (pentru unghiuri drepte în avioane ale proeminențelor și segmentele de dimensiuni originale);

2. Nivelul de conversie directă în linia proiectată (determinarea unghiului diedru, distanța între linii);

3. planul de transformare generică în planul proiectat (planul determinarea unghiurilor pe planul de proiecție, distanța de la punctul de la planul);

4. transforma planul la nivelul planului de proiecție (planul definit de dimensiunea reală).

Sistemul V1 H1 directă a soarelui (a se vedea. Figura 15) este proiectat la un punct. Segment k'1 l'1 - cea mai scurtă distanță între marginile AS și BC. Pentru a construi proiecția cea mai scurtă distanță în sistem V / H găsi conexiunea liniei punct l1 l1 k1 și de a efectua paralel cu axa X2 de proiecție, după care, prin intermediul liniilor de comunicație sunt principale kl de proiecție și k'l“.

Metodele REZUMAT rotație constă în faptul că forma geometrică predeterminată prin rotație în jurul unei axe se mișcă în spațiu, atâta timp cât acesta nu ia o anumită poziție în raport cu planurile nemodificate ale sistemului de proiecție.

În funcție de poziția axei de rotație în raport cu planurile de rotație ale proeminențelor sunt următoarele metode:

a) se rotesc în jurul axelor perpendiculare pe planele proeminentelor;

b) aceeași fără ca poziția axelor de rotație;

c) rotația în jurul orizontală sau frontal;

g) care se rotește în jurul unuia dintre piesele plane (aliniere).

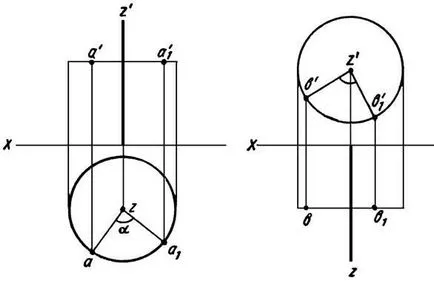
Figura 17 Figura 18

În diagrama (Figura 17) prezintă punctul A și rotirea axei Z, perpendicular pe planul H. proiecția Prin rotirea în jurul axei Z punctul A se va deplasa de-a lungul unei circumferințe situată într-un plan perpendicular pe axa de rotație (paralelă cu planul H al proiecțiilor). Dacă punctul E. Rotated A mutat din poziția A în poziția A1 r. În jurul axei sale Z la un unghi α. apoi proiecția orizontală (a) să preia poziția a1. în timp ce descrie o za raza arc (za - raza de rotație), și o vedere frontală (a „) a punctului se va deplasa de-a lungul unei a'a'1 drepte. paralelă cu axa X.

În cazul în care axa de rotație Z (Figura 18) este perpendicular pe planul de proiecție V, atunci punctul este rotit în jurul acestei axe, în proiecție frontală a traiectoriei se va muta circumferința și orizontală - linia paralelă cu axa X.

Exemplul 9. Pentru a combina punctul A și planul P, prin rotirea acestuia în jurul unei axe predeterminate Z (Figura 19).

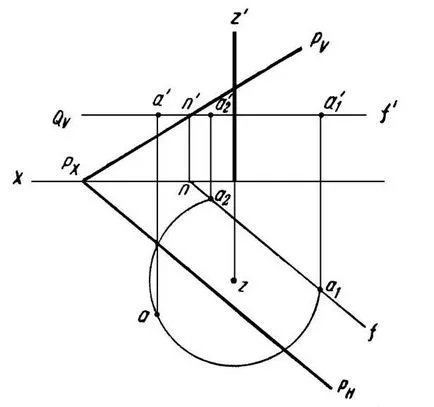
În timpul rotației în jurul axei Z, punctul A se va descrie un cerc plan Q. perpendicular pe această axă. Avionul Q intersectează planul P, la o NF orizontală predeterminată. Evident, punctul A va fi într-un plan P, atunci când cercul descris de punctul A intersectează NF orizontală. Sarcina, așa cum se arată, are două soluții.

Pentru a activa linia AB (figura 20), la un unghi α, suficient pentru a transforma cu un unghi predeterminat aparținând doi, ea punct. Din figură se observă că ABZ triunghiurile și z1 b1 a1 egale între ele (pe cele două părți și unghiul dintre ele), ci pentru că ele sunt egale, rezultă că ab = a1 b1, r. E. Valoarea proiecției orizontale a segmentului în timpul rotației sale în jurul axei, perpendicular H nu este schimbat, se schimbă numai poziția sa în raport cu axa de coordonate. Această situație face posibilă pentru a simplifica construcția de exemplu în abordarea

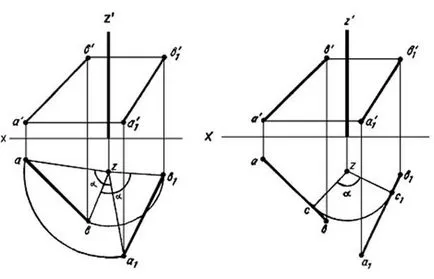
Figura 20 Figura 21

Figura 21 să se rotească în jurul liniei AB Z axa cu un unghi α z, omis perpendicular ab. Apoi, punctul este rotit cu un unghi predeterminat α, c1 punct printr-o linie este trasată perpendicular pe raza c1 z, iar segmentele întârziate c1 a1 = ca și b1 c1 = cb.

Rotirea planului în jurul unei axe perpendiculare pe planul de proiecție, se realizează prin rotirea în același unghi în aceleași puncte de direcție și linii, în care planul predeterminat.

Figura 22 plan definit de triunghiul ABC este rotit în jurul axei Z. o poziție perpendiculară pe planul frontal (proiecție orizontală poziția orizontală A1 luată perpendicular pe axa X).

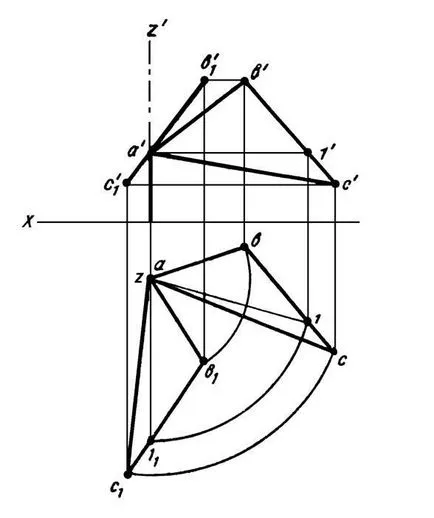
În cazul în care piesele plane specificate, apoi pentru planul de rotație, la un unghi trebuie rotit cu un unghi predeterminat de una orizontală sau urme și acest plan frontal (Figura 23).

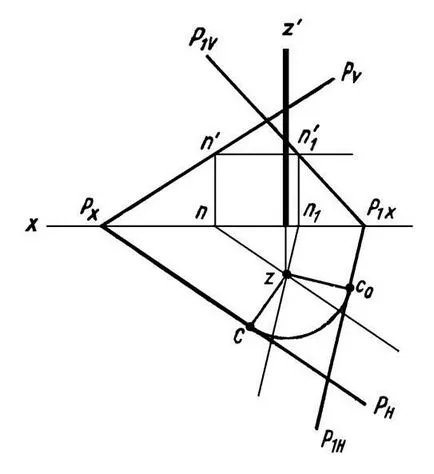
Astfel, în timpul rotirii orice formă spațială în jurul unei axe perpendiculare pe un plan de proiecție, proiecția acestuia pe planul de amploarea acestuia nu se schimbă. Se va schimba numai poziția de proiecție în raport cu axa de coordonate. Profitând de acest lucru, pentru o soluție la o problemă, putem aplica metoda de rotație, nu este prezentat în desen, axele de rotație.