Logaritmi exemple și soluții

După cum se știe, în multiplicarea expresii de gradul lor de performanță se adaugă întotdeauna (a b * a c = a b + c). Această lege matematică a fost derivat de Arhimede, iar mai târziu, în secolul VIII, matematicianul Virasen a creat tabela la fel de mult ca și performanță. Ei au servit la deschiderea în continuare a logaritmi. Exemple de utilizare a acestei funcții poate fi găsit aproape oriunde doriți să simplifice multiplicarea greoaie prin simpla adăugare. Dacă cheltui 10 minute pentru a citi acest articol, vom explica ce logaritmi și cum să lucreze cu ei. un limbaj simplu și accesibil.

Definiție în matematică

Logaritmul este o expresie a forma: Loga b = c, adică, logaritmul oricărui număr non-negativ (adică, orice pozitiv) „b“ a bazei sale de „a“ este considerat gradul de „c“, care este necesar pentru a construi o bază de „o“, astfel încât în cele din urmă obține valoarea „b“. Să luăm în considerare exemplele de jurnal, de exemplu, este o expresie log2 8. Cum de a găsi răspunsul? Foarte simplu, aveți nevoie pentru a găsi un grad care de la 2 pentru a obține gradul dorit 8. După ce a făcut niște calcule în minte, vom obține numărul 3! Și este adevărat, pentru că 2 la puterea 3 dă numărul de răspuns 8.

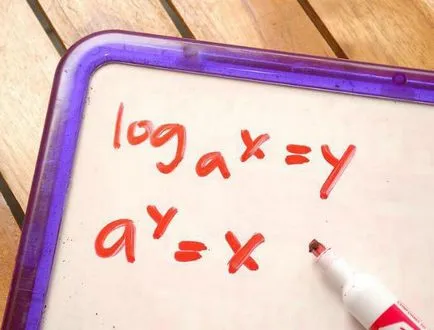
soiuri de logaritmi

Pentru mulți elevi și studenți, acest subiect pare complicat și confuz, dar în realitate, logaritmii nu sunt atât de teribil, principalul lucru - pentru a înțelege sensul general al ei și le amintesc proprietățile și unele dintre regulile. Există trei tipuri distincte de expresii logaritmice:

logaritm natural Într-o, în care baza este numărul lui Euler (e = 2,7).
Logaritm lg, in care un număr de bază este de 10.
Logaritmul oricărui număr b la bază a> 1.

Fiecare dintre ele se realizează prin mijloace convenționale, inclusiv o simplificare, reducere și reducerea ulterioară la un logaritm folosind teoremele logaritmice. Pentru credincioșii să-și amintească valorile logaritmilor proprietăților lor și ordinea acțiunilor în deciziile lor.

Reguli și anumite restricții

În matematică, există unele reguli, restricții, care sunt luate ca o axiomă, care nu este negociabil, și sunt adevărate. De exemplu, numărul nu se poate diviza de la zero, sau chiar imposibil de a extrage rădăcină chiar și gradul de numere negative. Logaritmi au propriile lor reguli, după care le puteți învăța cu ușurință cum să funcționeze, chiar și cu expresii logaritmice lungi și încăpător:

bază „un“ trebuie să fie întotdeauna mai mare decât zero și să nu fie egal cu 1, altfel expresia-ar pierde sensul, pentru că „1“ și „0“ la orice nivel este întotdeauna egală cu valorile lor;
în cazul în care un> 0, și b> 0, se dovedește că „un“ trebuie să fie mai mare decât zero.

Cum de a rezolva logaritmi?

De exemplu, având în vedere sarcina de a găsi răspunsul la ecuația x 10 = 100. Este foarte ușor, trebuie să alegeți un grad, care este ridicat la numărul zece, obținem 100. Este, desigur, gradul patratica! 10 februarie = 100.

Acum, să ne imaginăm expresia sub forma unui jurnal. Obținem log10 100 = 2. În rezolvarea logaritmilor toată acțiunea aproape imediat pentru a se asigura de a găsi, în măsura în care trebuie să intre în baza logaritmului pentru a obține un anumit număr.

Pentru determinarea fără erori a valorii nu este cunoscută măsura necesară pentru a învăța să lucreze cu puterile din tabel. Se pare, după cum urmează:

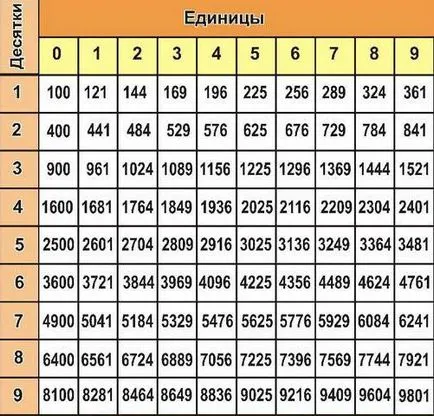
După cum puteți vedea, unele dintre exponenții poate ghici intuitiv, dacă aveți o minte tehnică și cunoștințe din tabelul de multiplicare. Cu toate acestea, pentru valori mari din tabel rata necesară. Se poate chiar și cei care nu absolut nimic despre utilizarea în teme matematice complexe. Coloana din stânga arată numărul (de bază a), rândul de sus al numerelor - o valoare a gradului de c, care este crescut numărul de un. La intersecția, valorile din numerele de celule sunt de răspuns (a c = b). Să luăm, de exemplu, prima celula cu numărul 10 și aduceți-l în pătrat, obținem o valoare de 100, care este indicată la intersecția a două dintre celulele noastre. Totul este atât de simplu și ușor de înțeles că, chiar și cele mai autentice umaniste!

Ecuații și Inegalitățile

Se pare că, în anumite condiții exponentul - aceasta este logaritmul. În consecință, orice expresie numerică matematică poate fi scrisă sub forma unei ecuații logaritmice. De exemplu, 3 4 = 81 poate fi scrisă ca logaritmul numărului 81 pe bază de 3, egal cu patru (log3 4 = 81). Pentru reguli puteri negative cum ar fi: 2 -5 = 1/32 scrise ca logaritm obține log2 (1/32) = -5. Una dintre zonele cele mai fascinante ale matematicii este tema „logaritmi“. Exemple și soluții de ecuații considerăm mai jos, imediat dupa ce a studiat proprietățile lor. Și acum să ne uităm la aspectul de inegalitate și cum să le distingă de ecuația.

Acesta este dat de următoarea expresie: log2 (x-1)> 3 - este inegalitatea logaritmică, ca valoare necunoscută „X“ este logaritmul. Și, de asemenea, în ceea ce privește compararea a două valori: logaritm numărului necesar de bază cu două mai mult decât numărul trei.

Cea mai importantă diferență între ecuațiile logaritmică și inegalitățile este că ecuațiile cu logaritmi (de exemplu - logarifm2 x = √9) este menit să răspundă la unul sau mai multe valori numerice, în timp ce în soluția de inegalitate este definită ca intervalul de valori admisibile și punctele de pauză această funcție. În consecință, răspunsul nu este un simplu set de numere individuale, în răspunsul din ecuație, și o serie continuă sau un set de numere.

teoreme fundamentale pe logaritmi

În rezolvarea sarcinilor primitive de a găsi valorile logaritmice ale proprietăților nu pot fi conștienți. Cu toate acestea, atunci când vine vorba de ecuații logaritmice și inegalități în primul rând, trebuie să înțeleagă în mod clar și să pună în practică toate proprietățile de bază ale logaritmi. Pentru exemple de ecuațiile vom învăța mai târziu, să analizăm mai întâi fiecare proprietate mai detaliat.

Identitatea de bază este după cum urmează: a = logaB B. Acesta se aplică numai în condițiile în care o este mai mare de 0, nu este egal cu una și B este mai mare decât zero.
Logaritmul produsului poate fi reprezentat prin următoarea formulă: logD (s1 * s2) = logD s1 + logD s2. În această condiție este: d, s1 și s2> 0; și ≠ 1. Se poate cita dovezi pentru această formulă logaritmi, și exemple pentru acest lucru. Să Loga s1 = s2 = f1 și f2 Loga. apoi o f1 = s1. un f2 = s2. Obținem că s1 * s2 = un f1 * o f2 = un f1 + f2 (proprietăți de grade), apoi prin definiție: LOGA (s1 * s2) = f1 + f2 = s1 + LOGA s2 LOGA, după cum este necesar.
logaritm private arata ca: LOGA (s1 / s2) = LOGA s1 - s2 Loga.
Teorema ca formula ia următoarea formă: q b n LOGA = n / q b LOGA.

Această formulă se numește „puterea de proprietate logaritm.“ Acesta seamănă cu un proprietăți convenționale de putere și nu este surprinzător, deoarece toate matematică se păstrează la postulatelor naturale. Să ne uităm la dovada.

Să Loga b = t, se obține un t = b. Dacă ambele părți erect în grade m: a tn = b n;

ci ca tn = (q) nt / q = b n. Prin urmare, q b LOGA n = (n * t) / t, atunci q b n LOGA = n / q b LOGA. Acest lucru dovedește teorema.

Exemple de probleme și inegalități

Cele mai frecvente tipuri de probleme pe logaritmilor - exemple de ecuații și inegalități. Ele se găsesc în aproape toate cărțile de probleme, precum și o parte necesară a examenului la matematică. Pentru admitere universitate sau examene de admitere în matematică este necesar să se știe cum să rezolve sarcini similare.

Din păcate, un plan comun sau schemă a deciziei și determinarea valorilor necunoscute ale logaritmului nu există, ci pentru fiecare inegalitate și ecuații matematice logaritmice se pot aplica anumite reguli. Mai întâi de toate ar trebui să aflați dacă este posibil să se simplifice expresia sau ca rezultat într-o vedere de ansamblu. Simplifica expresii logaritmice poate fi lung, dacă este corect de a folosi proprietățile lor. Să ne uităm la ele, mai degrabă.

În rezolvarea ecuațiilor logaritmice ar trebui să determine ce fel de logaritm în fața noastră: un exemplu al expresiei poate conține logaritmul natural sau zecimal.

Iată câteva exemple de logaritmi comune: ln100, ln1026. Soluția lor este de a se asigura că necesitatea de a determina măsura în care baza 10 va fi egală cu 100 și, respectiv, 1026. Pentru a face logaritmii naturale trebuie să aplice identități logaritmice sau proprietățile lor. Să arătăm câteva exemple de soluții logaritmică a problemelor de diferite tipuri.

Cum se utilizează logaritmul cu formula: cu exemple și soluții

Deci, ia în considerare exemplele teoremelor fundamentale ale logaritmi.

proprietate logaritm produs poate fi utilizat în sarcini în cazul în care este necesar pentru a descompune o valoare mare de b a unui prim-factori. De exemplu, log2 128 + log2 4 = log2 (4 * 128) = log2 512. Răspunsul este 9.
log4 8 = log2 2 2 3 = 3/2 log2 2 = 1,5 - după cum se poate vedea, folosind puterea a patra a proprietății logaritm, a fost capabil să rezolve expresie aparent complexă și nerezolvată. Este necesar doar să se descompună bază factorizarea și apoi face logaritmul valorii semnului.

Alocările UTILIZAREA

Logaritmi sunt adesea găsite în examenele de admitere, mai ales o mulțime de probleme în examenul logaritmică (examen de stat pentru toți absolvenții de liceu). De obicei, aceste sarcini sunt prezente nu numai în partea A (cel mai simplu test al examenului), dar, de asemenea, în partea C (sarcina cea mai complexă și voluminos). Examenul presupune o cunoaștere precisă și perfectă a subiectului „logaritm natural“.

Exemple de probleme și soluțiile sunt preluate din opțiunile oficiale de examen. Să vedem cum să rezolve astfel de sarcini.

log2 Dată (2x-1) = 4. Soluție:
rescrie simplificarea bit log2 sale (2x-1) = 2 2 pentru determinarea logaritmul obține că 2x-1 = 2 4. deci 2x = 17; x = 8,5.

Mai jos sunt câteva linii directoare de urmat, care pot rezolva cu ușurință toate ecuațiile care conțin expresii care sunt sub semnul logaritm.

Toate logaritmi cele mai bune conduc la o singură bază, soluția a fost greoaie și confuză.
Toate exprimare sub semnul logaritmului este prezentat ca un rezultat pozitiv, astfel încât atunci când se face o expresie de multiplicare exponent, care stă sub semnul logaritmului, și ca fundament acesteia, rămâne sub logaritmul expresiei trebuie să fie pozitiv.

Obosit de plictisitor fotografii de nunta? Utilizați aceste 10 idei de selecție de fotografii de nunta va ajuta să găsiți inspirație pentru cei care apreciază individualitatea și creativitatea. La urma urmei, unii tineri casatoriti nu sunt de acord pentru a converti lor.

11 calitati de sex feminin care oamenii găsi foarte atractive Faceți cunoștință cu trăsăturile feminine ale aspect pe care mulți bărbați par a fi deosebit de atractiv.