Lecția de algebra în clasa a 8-a de pe modulul și funcția pătratică

„Un mare număr de funcții
Oricine poate fi numit elev.
Dar numai câteva astăzi
Am decis să-ți spun "

Studiul modulului funcției pătratice vă permite să aprofundeze cunoștințele studenților în procesul de transformare a graficelor de funcții pătratice. Elevii cu mare interes pentru a îndeplini orice sarcină modul. Metodele de mai sus de diagrame caracteristici sunt comune și sunt utilizate nu numai în piață, dar, de asemenea, la alte funcții.

I. cuvânt introductiv al profesorului

Funcția - unul dintre conceptele matematice și științifice de bază, care exprimă relația dintre variabilele. Matematica are în vedere variabile abstracte, studiază legile relației lor, fără a adâncit în natura problemei. De exemplu, într-un raport de Y = X 2 sau un inspector matematician vezi dependență de suprafața unui pătrat pe o parte, și fizician, aeronave sau arhitect naval poate vedea relația Y forța de rezistență a aerului sau viteza apei din mișcarea X.

Math aceleași studii această dependență în formă abstractă și stabilește astfel încât în ​​creștere X 2 ori Y va crește de 4 ori, iar această concluzie poate fi aplicată în orice situație particulară.

Modul și o funcție pătratică

Trasarea funcții:

1. Y = AX + BX 2 + C,
2. Y = AX + BX 2 + C,
3. Y = Ax 2 + Bx + C

II. muncă orală

1) Definiți numărul modulului X

2) Definiți o funcție pătratică, spune tot ce se știe despre această funcție (grafic proprietăți).

3) Găsiți figura graficul Y = X + 4X cu 2 - 3.

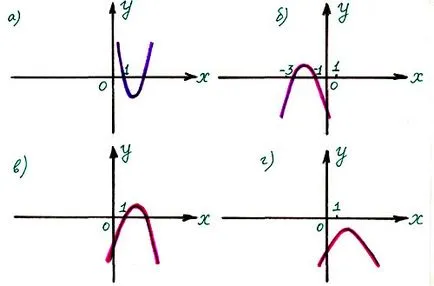
4) La ce ilustrează graficul Y = - (X + 1) (2 - x)?

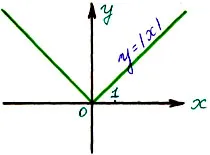
5) Nu uitați cum să construiască graficul Y = X

Prin definiție modul

Graful Y = X este simetric față de axa Y.

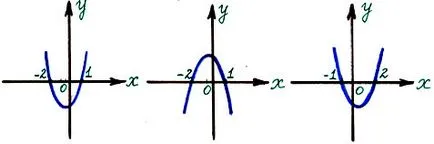
III. Trasarea funcții:

Activitatea desfășurată în grupuri, deoarece grafică în K-1) și K-3) sunt aceleași, ele trebuie să compare și să tragă o concluzie (din 3 grupe). Fiecare grup este emis un card în ea 3 locuri de muncă. Studenții trebuie să construiască grafice de funcții pătratice care conțin modulul, folosind definiția modulului și să încheie: cum să construiască un grafic al funcției, folosind graficul unei funcții pătratice și simetrie în raport cu axele de coordonate.

Sarcină. construi un grafic al funcției folosind:

a) definirea modulului;
b) Graficul funcției Y = Ax 2 + Bx + C;
c) în raport cu axele de simetrie.

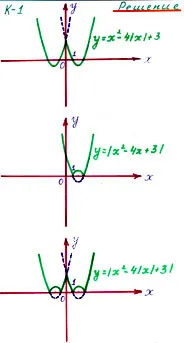
a) Y = X 2 - X 4 + 3
b) Y = X 2 - X 4 + 3
a) Y = X 2 - X 4 + 3

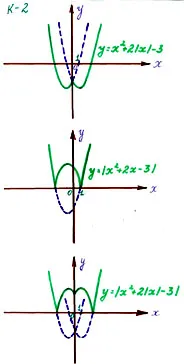
a) Y = X 2 + X 2 - 3,
b) Y = X 2 + X 2 - 3,
a) Y = X 2 + X 2 - 3,

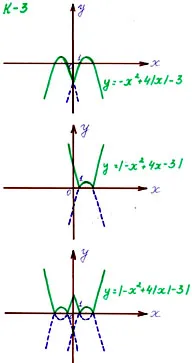
a) Y = X + 2 X 4 - 3
b) Y = X + 2 X 4 - 3
a) Y = X + 2 X 4 - 3

IV. Elevii încheie grafice de amenajare a acestor funcții

Întrebare: a) Cum de a construi un grafic al funcției Y = f (X)?

(Metoda 1. Se trasează funcția Y = f (X), în cazul în care X 0 și Y = f (-x), atunci când X <0.
2 metodă. Se trasează funcția Y = f (X) și afișajul din partea dreaptă a generat în mod simetric față de axa Y).

b) Cum de a construi un grafic al funcției Y = f (X)?

(Se trasează funcția Y = f (X) și punctul cu display ordonata negativ simetric față de axa X).

c) Cum de a construi un grafic al funcției Y = f (X)?

(Se trasează funcția Y = f (X), atunci când X este 0, iar această parte a ecranului grafic simetric în raport cu axa Y, iar apoi negativ afișarea coordonatelor punctului simetric în raport cu axa X.)

d) De ce funcțiile grafice Y = -x 2 + 4X - 3 și Y = X 2 - 4X + 3 sunt la fel?

(De la A = A -A = A)

Considerăm funcția a fost o variabilă independentă pentru marca modulului. Acum, ia în considerare funcția în cazul în care nu există nici o funcție în sine sau funcția, și variabila independentă la un moment dat, adică semnul modulului în funcție de tipul

Y = AX + BX 2 + C și Y = AX + BX 2 + C

Dă exemple specifice.

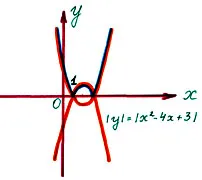
Se trasează Y = f funcție (X) și luând partea care este situată deasupra axei X ca X 2 - 4X + 3 0 și se adaugă la aceasta axa de cartografiere relativ simetric X. sale

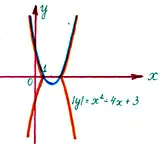
În primul rând, să construiască graficul Y = X 2 - 4X + 3. urmat de setul de puncte ale căror coordonate satisfac condiția Y = X 2 - 4X + 3. adică graficul Y = X 2 - 4X + 3 prezintă axa X. relativă

VI. Activitatea de creație

Funcția dată este Y = X 2 + 2X- 3

Rulează toate transformările posibile ale funcției pătratice cu modulul.