Gradul de libertate al solidului - studopediya
cinematica corp rigid
Absolut corp solid numit corpul material, forma geometrică și dimensiunile care nu se modifică în nici o acțiune mecanică din partea altor organe, iar distanța dintre oricare două dintre punctele sale rămân constante.
cinematica corp rigide, precum și dinamica corpului rigid, este una dintre cele mai dificile secțiuni ale cursului mecanicii teoretice.
corp rigid cinematicii problemă se încadrează în două părți:
1. Sarcina de mișcare și determinarea caracteristicilor cinematice ale mișcării a corpului în ansamblu;
2. Definirea parametrilor cinematici (traiectorie, viteză și accelerație) de deplasare a punctelor corpului individuale.
Există cinci tipuri de mișcare a corpului rigid:
1. mișcare de translație;
2. Rotirea în jurul unei axe fixe;
3. mișcare plană;
4. Rotația în jurul unui punct fix;
5. libera circulație.
Primele două sunt numite pur și simplu un mișcări ale corpului rigid:
Numărul masiv de grade de libertate este numărul de parametri independenți, care sunt determinate în mod unic poziția corpului în spațiu în raport cu cadrul considerat.
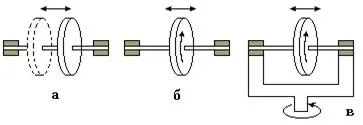
de mișcare a corpului rigid depinde în mare măsură de numărul de grade de libertate.
Să considerăm un exemplu. (. Figura a) Dacă discul nu se rotește, poate aluneca de-a lungul fixat în axa sistemului de referință, în sensul că acesta este cadrul de referință, în mod evident, are un singur grad de libertate - poziția discului este unic determinată, de exemplu, x coordonata centrului său, măsurat de-a lungul axe. Dar dacă te conduce, în plus, poate fi rotit (Fig b.) Devine încă un grad de libertate - de a coordona x j se adaugă la unghiul de rotație în jurul axei discului. (. În Figura) Dacă axa discului este fixată într-un cadru care se poate roti în jurul unei axe verticale, numărul de grade de libertate este egal cu trei - j la x și unghiul de rotație cadru adăugat f.
Punct de masă liber în spațiu are trei grade de libertate: cum ar fi coordonatele carteziene x, y și z. Coordonatele punctelor pot fi, de asemenea, determinată în cilindric (r, j, z) și sistemele de referință sferice (r, j, f), dar numărul de parametri care determină în mod unic poziția unui punct în spațiu este întotdeauna trei.
Punctul de material în planul are două grade de libertate. Dacă planul XOY alege un sistem de coordonate, x și Y coordonatele definesc poziția punctului în plan, iar z este identic coordonatei zero.
Punct de material gratuit de pe suprafața de orice fel are două grade de libertate. De exemplu: poziția pe suprafața Pământului este definită de doi parametri: longitudine și latitudine.
punct material pe o curbă de orice fel are un grad de libertate. Parametrul determinarea poziției unui punct de pe curba poate fi, de exemplu, distanța de-a lungul curbei de origine.
Luați în considerare două puncte materiale în spațiu, conectate printr-o tijă rigidă lungime l. Poziția fiecărui punct este determinat de trei parametri, dar se impune relația lor.
Ecuația este o ecuație de comunicare. Din această ecuație, oricare dintre coordonate pot fi exprimate în termeni de cinci coordonate rămase (cinci parametri independenți). Prin urmare, aceste două puncte sunt () cinci grade de libertate.
Luați în considerare trei puncte materiale în spațiu, care nu se află pe o linie dreaptă, conectate prin trei tije rigide. Numărul de grade de libertate a acestor puncte este egal cu () șase.
corp rigid gratuit are, în general, de șase grade de libertate. Într-adevăr, poziția corpului în spațiu în raport cu un sistem de referință este definit prin specificarea sale trei puncte care nu se află pe o linie dreaptă, iar distanța dintre punctele într-un solid rămân neschimbate în toate mișcările sale. Conform celor de mai sus, numărul de grade de libertate trebuie să fie egal cu șase.