Funcția x ^ y și y 2 x 3 grafice, funcțiile și proprietățile
Funcția y = x ^ 2 este numită o funcție pătratică. Graficul funcției pătratică este o parabolă. Forma generală a parabolei este prezentată mai jos.
funcţia pătratică
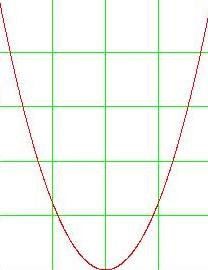
Figura 1. Vedere generală a parabolei
După cum se poate vedea din grafic, este simetrică față de axa y. Axa Y se numește axa de simetrie a parabolei. Acest lucru înseamnă că, dacă țineți linia pe grafic paralel cu axa x este axa de cele de mai sus. Se intersectează parabolei în două puncte. Distanța între aceste puncte la axa y este același.
Axa de simetrie împarte graficul parabolei ca și în cazul în care în două părți. Aceste componente sunt numite ramuri ale parabolei. Un Parabola care punct se află pe axa de simetrie se numește vârful parabolei. Aceasta este, axa de simetrie trece prin vârful parabolei. Coordonatele acestui punct (0; 0).
Proprietățile de bază ale unei funcții pătratice
1. Când x = 0, y = 0 și y> 0 dacă x0
2. Valoarea minimă a unei funcții pătratice atinge apogeul. Ymin când x = 0; De asemenea, trebuie remarcat faptul că valoarea maximă a funcției nu există.
3. Funcția diminuează în intervalul (-∞, 0] și creșteri în intervalul [0; + ∞).
4. Valoarea x opusă corespunde aceleiași valori y.
funcţia cubic
Funcția y = x ^ 3 se numește o funcție cubi. Programeaza o funcție cubică este numit un parabole cub. Forma generală a parabolei este prezentată mai jos.
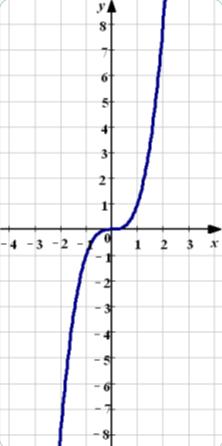
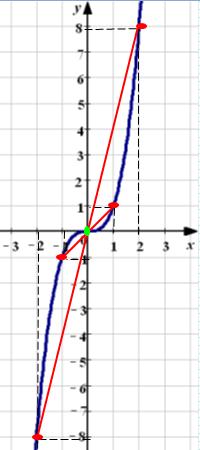
Proprietăți funcționale Cubic
Lista proprietățile de bază ale funcției cubice
- Când x = 0, y = 0. y> 0 pentru x> 0 și y
- Într-o funcție de cub nu există, nu este valoarea maximă sau minimă.
- Funcția de cubice crește pe întreaga axă (-∞; + ∞).
- Valorile opuse x corespunzătoare opuse y.