Formula de forța de atracție în fizică
Între toate organismele care au mase, forțe care atrag organismul menționat mai sus unul de altul. Aceste forțe se numesc forțe de atracție reciprocă.
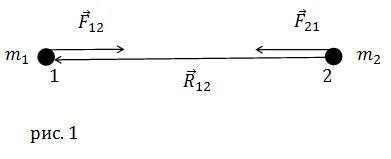
Luați în considerare două puncte materiale (Figura 1). Ele sunt atrase de forțele direct proporționale cu produsul masei particulelor și invers proporțională cu distanța între acestea. Astfel, forța gravitațională () va fi egal cu:
m2 unde materialul actele punct în masă pe m1 masa punctului material cu forța gravitației - raza - vector, care are loc de la punctul 2 la punctul 1, modulul acestui vector este egală cu distanța dintre punctele de material (r); G = 6,67 • 10 -11 m 3 kg -1 s -2 (unități SI) - gravitate constantă (constanta gravitatiei).
Potrivit lui Newton legea a treia a forței cu care punctul de material 2 este atras de punctul de material 1 () este:
Atracție între organismele se realizează prin intermediul câmpului gravitațional (câmp gravitațional). Forțele gravitaționale sunt potențial. Acest lucru face posibilă introducerea unei astfel de energie caracteristică câmpului gravitațional ca potențial, care este raportul dintre energia potențială a unui punct material, situat la domeniul investigat la greutatea unui anumit punct.
Formula pentru forța de atracție a corpurilor de formă arbitrară
Cele două corpuri de formă și mărime arbitrară selectați masa elementară, care pot fi considerate puncte materiale, în care:
în care - densitatea substanței punctelor de masă ale primului și al doilea corp, DV1, DV2 - volumele elementare ale punctelor selectate materiale. Într-un astfel de caz, forța de atracție (), element acționează asupra elementului dm2 DM1. este egal cu:
Prin urmare, forța de atracție a doua a primului corp poate fi găsit prin formula:
în cazul în care este necesară integrarea pentru a face întregul volum pe primul (V1) și corpurile a doua (V2). În cazul în care corpurile sunt omogene, atunci expresia poate fi un pic de conversie și obțineți:
Formula pentru forța gravitațională a solidelor de formă sferică
În cazul în care forțele de atracție sunt luate în considerare pentru cele două corpuri solide de formă sferică (sau aproape de bile), densitatea care depinde de distanțele până centrele cu formula (6) devine:
unde m1, m2 - masa de bile - raza - vectorul care leagă centrele de bile,
Expresia (7) poate fi utilizat în cazul în care unul dintre organismele are o alta decât sferică forma, dar dimensiunea sa este mult mai mică decât dimensiunile de al doilea corp - glob. Astfel, formula (7) pot fi utilizate pentru calculul forțelor de atracție a corpurilor spre Pământ.
Unități forțelor de atracție
Unitatea de bază de măsurare a forței de atracție (sau orice altă forță) în unități SI este: [] = H.
Exemple de rezolvare a problemelor
Sarcină. Care este forța de atracție între două mase omogene identice de minge, care este egală cu 1 kg? Distanța dintre centrele lor egal cu 1 m.
Decizie. Baza de calcul este utilizat pentru rezolvarea problemei:
Pentru a calcula forța de atracție a modulului (1.1) este transformata in:
Sarcină. Cu ce forță (în valoare absolută) este infinit lung și subțire și bar drepte atrage o particulă de material de masă m. Particula este distanțat de o tijă. Densitatea liniară a masei de material a tijei este tau
Decizie. face un desen
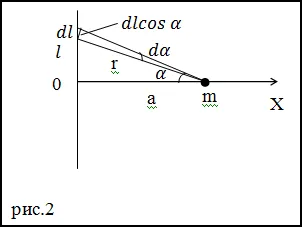
Selectăm pe site-ul Web dm masa elementară:
O forță de atracție între elementul selectat pe tijă și punctul de material poate fi găsit ca:
este evident din figura 2 că:
Substituind expresia (2.3) (2.2), avem:
Fig. 2 arată că:
Membru supleant pe partea dreaptă a (2.5) la (2.4), obținem:
Pentru forța cu care particula este atras de bar, petrece integrarea expresiei (2.6). Limitele de integrare alege între 0 pi / 2, deoarece expresia nesfârșită tijă multiplică două integrare a fost realizată pe parcursul întregului volum al tijei.