amortizare vibrații și vibrații
B și b r o r a n e w și e.Vibrogashenie este un proces pentru a elimina vibrațiile obiectului, fără a elimina sursele acestor vibrații. Unele dispozitive tehnice elimina sursele de oscilație, de exemplu, prin solduri, din diverse motive imposibile. Cu toate acestea, există o necesitate pentru călire oscilații ale dispozitivului în ansamblu. Pentru a rezolva această problemă, puteți aplica așa-numitul umezire vibrații activ. elemente care funcționează pe principiul sistemului de control automat (ACS). O altă opțiune este utilizarea soluțiilor de absorbție a vibrațiilor pasive, care se realizează printr-un așa-numitele amortizoare de vibrații dinamice sau amortizoare de vibrații dinamice fiind conectat la dispozitivul din exterior printr-o conexiune elastică.

- frecvența circulară - timp.
Atașați la valoarea unitară a masei suplimentare 2 printr-un coeficient de rigiditate elastică. poziția masei de coordonate este determinată.
Pentru a obține ecuațiile diferențiale ale mișcării maselor 1 și 2 utilizarea ecuației Lagrange II genus:
în care - energia cinetică a sistemului de masă, - energia potențială a sistemului, - coordonate generalizate - rata generalizată (derivata coordonatelor generalizate în timp); - forța generalizată. Acest sistem are două grade de libertate, astfel încât i se poate prinimattolko două valori.
Energia cinetică a sistemului este determinată de suma maselor și energiile cinetice. .
Energia potențială este dată de următoarea expresie.
Noi definim termenii ecuației Lagrange
forță generalizată acționează numai asupra greutății.
termeni gasit putea permite obținerea următorul sistem de ecuații diferențiale:
Aceste ecuații descriu mișcarea de vibrație a obiectului 1 și absorbantul 2. Deoarece vibrațiile obiectului cu masa sunt deplasate, ele apar cu o frecvență a forței motrice P și sunt descrise de aceeași ecuație, adică
Diferențierea de două ori aceste expresii, obținem
Substituind în ecuațiile diferențiale în locul coordonatelor și al doilea derivatele expresiilor obținute, după reducerea corespunzătoare se pot scrie
Soluția acestui sistem de două ecuații este determinarea algebrică a amplitudinilor și. Ne exprimăm a doua ecuație
și substituie rezultatul în prima ecuație a sistemului. Apoi, se obține o ecuație care conține numai o singură necunoscută:
Dacă numitorul expresiei obținut echivalează cu zero, atunci această egalitate se numește ecuația de frecvență și rădăcinile sale sunt egale cu frecvențele la care amplitudinea obiectului tinde la infinit. Această stare a sistemului corespunde rezonanță.
Dispariția amplitudinii are loc la zero, expresia din paranteze în numărătorului, și anume. În cazul în care se produce acest fenomen, masa suplimentară (amortizor de masă) variază într-un mod de rezonanță, deoarece frecvența forței motrice coincide cu frecvența propriilor oscilații. În același timp, masa obiectului în sine rămâne staționară. Acest fenomen se numește antiresonance. Este utilizat pentru amortizarea oscilațiilor obiectului la o forță stabilă de conducere frecvență prin selectarea adecvată a masei de absorbție și coeficientul său de rigiditate a elementului elastic.
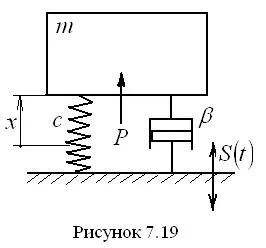
Baza oscilează în plan vertical, în conformitate cu o anumită lege. În acest caz, un obiect acte de forță variabilă. în funcție de deplasarea obiectului și viteza acestuia.
Ecuația de mișcare obiect are forma de vibrație la baza
Această ecuație corespunde formei cunoscute în mecanică teoretică, ecuația de bază a dinamicii, în care funcția de pe partea dreaptă este egală cu suma forțelor care acționează asupra sistemului. Această sumă poate fi exprimată ca. în cazul în care primul termen este forța elastică a arcului, al doilea - forța de rezistență (forța de frecare) suspensie. Semnul negativ de pe partea dreaptă indică acțiunea opusă a acestor forțe în raport cu direcția obiectului.
Substituind suma rezultată în partea dreaptă a ecuației, după împărțirea prin transformări simple și au
În această ecuație. A măsurat. - pătratul frecvenței oscilațiilor naturale ale obiectului, măsurate în. Partea dreaptă a ecuației este derivata a doua a oscilațiilor obiect de excitație cinematice la partea de bază. Ea poate fi înlocuită cu o atitudine. în cazul în care - o forță externă care variază în armonie, adică. Apoi ecuația anterioară devine
Această ecuație este ecuație diferențială neomogenă a cărei soluție este cunoscută ca fiind egală cu suma soluțiilor omogene ale ecuației (excluzând partea dreapta) și o soluție particulară a acestei ecuații. Soluția generală a ecuației omogene pot fi omise datorită faptului că determină vibrațiile naturale ale obiectului, care se estompeze rapid. O soluție special pentru oscilația la starea de echilibru obținută ca
în care - forța de deplasare de fază și de deplasare este determinată de expresia
Diferențierea de exprimare în ceea ce privește timpul da
Acum definim puterea transmisă de obiectul de bază
Multiplicatorul poate fi divizat înainte de parantezele și se înmulțește cu. atunci acesta poate fi reprezentat ca raportul dintre amplitudinea deplasării vibrațiilor forțate la deplasarea maximă datorită forței statice, egale. Acest raport se numește coeficientul dinamic și determinat prin formula
Coeficientul de cosinusul în paranteze pătrate pot fi reprezentate sub forma și marcați tangenta un anumit unghi. adică. Apoi, acest coeficient poate fi înlocuit cu o tangentă, și după transformările corespunzătoare expresiei în paranteze modificări sinusul unghiului sumei, adică.
Rezultând într-un factor în ceea ce privește forța și înlocuită cu expresia finală pentru calculul forțelor
(Vârf) Valoarea maximă a forței este egală cu sinusul expresiei, adică,
Raportul dintre cea mai mare forță transmisă de obiectul de bază pentru amplitudinea forței de excitație este denumit raportul de transmisie a forței. În acest caz,
Din ultima formulă este clar că are loc egalitate numai atunci când. adică în absența amortizării.
Factor de transmisie a puterii caracterizează calitatea sistemului de vibrații dovada. Când compusul obiectului hard depreciat și o bază. Atunci când sistemul de vibrații dovada este eficientă atunci. atunci când se aplică suspendarea este imposibil deoarece duce la o creștere a forței transmise.
Studiile arată că, în scopul de a forța valoarea a fost mai mică decât amplitudinea forței motrice trebuie să fie condiția. De obicei, este nevoie Aceasta înseamnă că pentru o protecție eficientă a obiectului de la baza oscilațiilor (amortizare obiect eficient), este necesar ca frecvența naturală a sistemului a fost semnificativ mai mică decât oscilații de frecvență de bază.
Testați-vă cunoștințele
1. Care este efectul dezechilibrului al maselor în rotație în sistemele mecanice dure și nerigidă?
2. Care sunt cauzele dezechilibrului unităților de rotație?
3. Care sunt efectele forțelor neechilibrate pe fundația mașinii?
4. Numele și descrie tipurile de dezechilibre ale unităților de rotație?
5. eliminarea dezechilibrului static și de echilibrare statică, echilibrarea dinamică și dezechilibru?
6. Cum soldurile necesare pentru echilibrarea statică, echilibrarea dinamică, și de ce?
7. Cum este înlocuirea masei a tijei de legătură într-două mase de puncte?
8. Cum se chetyrohsharnirnogo mecanismul de echilibrare statică?
9. În ce fel se realizează mecanism slider-manivelă tapiterie?
10. Care este mecanismul de auto-echilibrat?
11. Cum echilibrării parțială în mișcare translationally mase mecanism slider-manivelă?
12. Care este woodcore? Care este principiul amortizorului dinamic?
13. Ce este de izolare a vibrațiilor? Cum este protecția obiectului de la baza de oscilație?
14. Care este factorul dinamic, coeficientul de transmisie a puterii?
15. În ce stare se obține o protecție efectivă a obiectului de la baza oscilatiei?