Volumul paralelipiped dreptunghic este egală cu 2,520 cm (un cub) și suprafața de bază 168 cm (pătrat

Chiar și desen nu este necesar, deoarece este rezolvată vocal.

Deci, ce este volumul cutiei? Vpar Sosn = * H, unde H este una din coastele noastre și toate 4. Arată figura mai târziu.

Așa că am găsit o margine. Acesta a părăsit celelalte două, care sunt obținute prin bazele lor.

Sosn = a * b; unde a, b - partea de bază a paralelipipedului.

Este cunoscut faptul că a = b + 2

Deci, adevărat este:

Soluția ecuațiilor pătratice, rapid și ușor.

Răspuns: b1 = 12; b2 = -14 (nu poate fi atât un negativ)

Prin urmare, b = 12; a = 12 + 2 = 14

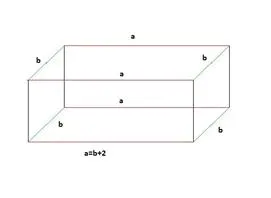
Pentru claritate, am desemnat special de margine este o culoare roșie. Edge b în verde, și înălțimea H a cernelii rămase.

Se pare că numai un paralelipiped cu 4 fiecare nervură. Aceasta este logic să se scrie că suma va fi egală cu:

Suprafața bazei piramidei este egală cu 108 dm 2, iar înălțimea - 24 dm. Secțională piramidă plane de bază paralelă au zone 48 și 75 dm3. Găsiți distanța dintre planurile ale secțiunilor transversale.

Deci avem o abecedarele piramidă (triunghiular pictat, pentru că în această sarcină, nu există nici o diferență)

De asemenea, trage două secțiuni DFE și D1F1E1 plan paralel ABC.

Acum vedem că avem o piramidă similară. Să ne uităm la ordinea:

1) Piramida DfES va fi similar cu abecedarele piramidale. Conform regulii zonelor de similaritate S (# 916; ABC) / S (# 916; DFE) = k2

După ce a găsit un coeficient de similaritate, putem găsi înălțimea piramidei DfES.

108/48 = 2,25 → k = √ (2,25) = 1,5

Acum, amintiți-vă că înălțimea laturilor au cifre similare în ceea ce privește primi k = h1 / h2

Deci înălțimea noastră este egală cu 24 / h (DfES) = 1,5 → h (DfES) = 24 / 1,5 = 16

2) In mod similar D1F1E1S piramidă similară cu ABCs. Să ne găsim înălțimea sa, în același mod.

24 / h (D1F1E1S) = 1,2 → h (D1F1E1S) = 24 / 1,2 = 20

3) Avem nevoie de distanța față de planul la DFE D1F1E1. Acesta va fi egal cu 20-16 = 4 dm.

Baza piramidei - un triunghi isoscel cu un unghi la vârf # 945; și raza R. cerc circumscris Cele două fețe laterale inegale perpendicular pe planul de bază, iar a treia fata este înclinată la acesta la un unghi # 946;. Localizați suprafața laterală a piramidei.

Figura arată abecedarele piramida, din vârful S vedena apotemă SK ave AC la baza unui triunghi isoscel. Toate acestea vom avea nevoie pentru a rezolva această problemă.

Deci, raza cercului descrierii poate fi găsit ca:

R = a / 2sin # 945; → CB = a = R * 2sin # 945;

Acum CB partea Cunoscându găsi cealaltă parte AC și AB, care sunt egale între ele.

Să scrie ce zone constituie suprafața laterală:

Acum trebuie să picteze cum să găsească fiecare dintre ele.

Regulate Segmentul de piramidă triunghiulară care leagă baza cu înălțimea medie a apotemă piramidei, m este egal cu înălțimea și formează o piramidă, unghiul # 946;. Găsiți suprafața completă a piramidei.

Imaginea arată o piramidă ACBO, OM-înălțime, OK-apotemă.

Mid punctul L apotemă OK, LM formează un unghi cu înălțimea OM # 946;.

# 916; OMK dreptunghiular, prin urmare, ML este mediana triunghiului, atunci OL = LM = LK = m

# 916; isoscel OLM De aceea ∠OML = ∠LOM, ceea ce înseamnă că formele unghiulare cu apotemă înălțime # 946; (Prezentat).

Sbok = p • un / 2; unde p - bază semiperimetrul, o - apotemă OK.

La baza piramidei noastre este un triunghi dreptunghic ale cărui laturi sunt egale. Să ne găsim marginea bazei, pentru aceasta folosim datele deja disponibile. După cum este cunoscut MK este raza înscrisă în cercul de bază.

r = AB * √ (3) / 6 → AB = 6r / √ (3)

Vom găsi ceea ce este r, știind că păcatul # 946; = MK / OK → OK = MK / păcat # 946; = 2m / păcat # 946;