vector axial

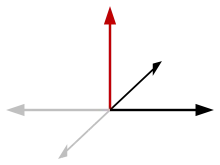
După inversarea celor doi vectori schimbă semnul, dar produsul lor vector rămâne neschimbat.

vector axial (axial liniei centrale Engl ..) sau pseudo - cantitatea ale cărei componente sunt transformate cu vectorul rotației sistemului de coordonate, dar se schimba semnul este opus comportamentului componentelor vectorului în orice inversare (circulație semn) coordonează. Ie pseudo inversează menținând valoarea absolută (este înmulțită cu un minus) la orice inversare a sistemului de coordonate.

Pentru a evidenția diferența dintre vectorul prezent ale cărui coordonate sunt întotdeauna convertite precum și coordonatele unui vector de mișcare, acest vector este numit vector adevărat sau polar.

Cel mai simplu exemplu al unui vector axial în spațiul tridimensional este un produs vectorial al vectorilor de două polarități, de exemplu, în mecanica - unghiular impuls L = r × p = \ mathbf \ ori \ mathbf

>. în spațiu cu patru dimensiuni - axial curent.

Când transformarea de coordonate de coordonate vectorul axial obținut prin înmulțirea unui factor suplimentar (-1) în comparație cu adevărata transformare de coordonate (altfel denumit polare) vectori, în cazul în care baza se schimbă orientarea (de exemplu, în cazul în care baza este supusă reflexie). Aceasta, împreună cu un pseudoscalari. un caz special de pseudo. Înfățișată în această grafic pseudo coordonate înfrîngeri schimbare.

• Geometria reprezentare aplicare pseudovec- cel mai utilizat pe scară largă poate fi cu ajutorul tridimensional de rotație infinit de mici. Probabil (?), Vectorul Termenul axială este tocmai aici, deoarece pseudo definește o axă de pivotare (direcția), dar numai până la un factor de (± 1), cu direcția de rotație a alegerii arbitrare condiționată asociat bazei drept, spre deosebire de adevărat ( polar) vector care reprezintă segmentul direcționat (sau translație paralelă) pornire destul de clar specificate și fără ambiguități și puncte finale.

Modul obișnuit de a genera pseudovectors pseudovectorial această operațiune, cel mai frecvent, dacă nu singurul utilizat în mod obișnuit în cazul tridimensional este produsul vectorial (așa cum se obișnuiește în notația de coordonate include Levi-Civita pseudo) operație și care conține produsul vectorial (de exemplu, rotor etc. ). sau un număr impar de ele. operațiune Pseudovector generează adevărate de vectori și scalari pseudovectors și pseudoscalars.

Deci, atunci când este multiplicată cu vectorul adevărat al vectorului adevărat - este obținut în produsul scalar un scalar și vectorial produs adevărat - pseudo. Când înmulțirea unui vector cu un produs pseudoscalari real, se obține într-un pseudoscalari și produsul vectorial al unui vector adevărat. Când înmulțirea două pseudovectors - obținut în mod corespunzător adevărat scalară și pseudo.

Teoriile fizice, cu excepția celor în care există un distinct și observabile în principiu pseudovectors spațiu de simetrie în oglindă poate fi prezentă în valorile intermediare, dar în final observate - Multiplicatorii (-1) la reflectarea în oglindă a coordonatelor trebuie eliminate, reuniți în lucrările chiar număr de ori (chiar și numărul de pseudovector pseudoscalari + + alți factori pseudotensorial).

• De exemplu, în electrodinamică clasice inducției magnetice - pseudo au fost generate operație pseudo-, de exemplu, j x r \ ori \ mathbf \> drept Biot-Savart. dar valoarea acestui (pseudo) determinată, în principiu, până la multiplicator condiționată, care poate fi selectat +1 sau -1. Cu toate acestea, valoarea reală observată - accelerația taxa sub efectul câmpului magnetic - în cazul în care calculul său cuprinde o altă operațiune pseudovector v × B \ ori \ mathbf \> în expresia forței Lorentz. oferind un alt factor condițională ± 1, egal cu primul, răspunsul este arbitrar dispare, deoarece produsul de ± 1 · (± 1) dă un 1.
• Mecanica pseudovector valoare apar cel mai frecvent - viteza unghiulară și asociate (de exemplu, un moment unghiular). Vectorul viteză adevărată este obținută de la o viteză unghiulară ω pseudovec- \> pseudo- funcționare ω × r \ ori \ mathbf \>.