Unghiul de clasa Math 10 între liniile din spațiu

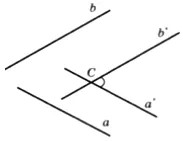
Unghiul dintre cele două linii drepte care se intersectează este măsurată în același mod ca și în planimetrie (deoarece prin aceste linii pot fi făcute plane). Astfel, unghiul dintre două linii care se intersectează în spațiu este cea mai mică dintre unghiurile formate de razele acestor linii cu vârful în punctul de intersecție.

Unghiul dintre cele două linii paralele este considerată a fi 0 sau 180 °.

Unghiul dintre două linii drepte care traversează a și b este definită după cum urmează: prin orice punct C se realizează a'i grinzi b „astfel încât || a „și b || b“. Apoi, unghiul dintre o „și b“ este luat egal cu unghiul ab. Cu alte cuvinte, liniile A și B sunt transferate într-o nouă poziție paralelă cu ei înșiși înainte de a traversa. În special, punctul C pot fi luate pe una din liniile a și b, care în acest caz este fix.

Astfel, unghiul dintre liniile se numește unghiul oblic între linii intersectate, respectiv, date paralele.

linii perpendiculare în spațiu

Două linii sunt numite ortogonale în spațiu, în cazul în care unghiul dintre ele este 0-90

Lema: În cazul în care una dintre cele două linii perpendiculare pe o a treia linie, cealaltă linie perpendiculară pe această linie.

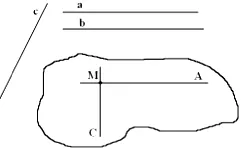
După t. M (M o, M și M c) să efectueze MA direct și MC || a || c. Deoarece o cu (prin ipoteză), atunci AMC = 90o. Prin condiția unei || b și MA || a (prin construcție) înseamnă, b || MA (pentru teorema trei linii paralele). Apoi, liniile b și c sunt paralele, respectiv MA și MS, unghiul dintre care 90º b c, după cum este necesar.

Această linie se numește perpendicular pe planul în cazul în care este perpendicular pe orice linie dreaptă situată pe planul.

(Poate înregistra: a α sau α a).

O linie dreaptă perpendiculară pe planul intersectează planul.

și alfa a b, a c, o d.

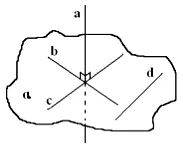
Dacă una dintre cele două linii paralele perpendiculare pe planul, iar cealaltă linie este de asemenea perpendicular pe acest plan.

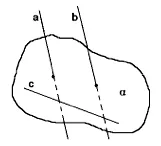
Egal în plan a de la o linie arbitrară. Deoarece un α, și apoi cu (prin definiție). Prin Lema, dacă o c perpendicular, și b, precum și paralel cu perpendiculara. Deoarece c - linie dreaptă arbitrară și este perpendicular pe gruparea a (prin definiție). QED.

Dacă 2 linii sunt perpendiculare pe planul, atunci ele sunt paralele.

În cazul în care o linie nu se află într-un plan perpendicular pe două linii care se intersectează într-un plan, atunci linia dreaptă și planul perpendicular.

m α, n α, m n = 0,1 m, 1 n

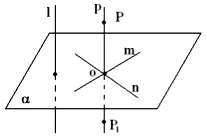
Trage o linie p astfel încât G p și p || 1. N 1 și p 1 || p n și p m. Fie P și P1 - punctul linia p astfel încât OP = OP1. Apoi, m și n - și deci axa de simetrie, α - planul median de simetrie a acestor puncte, și, prin urmare p a. și p p α || 1 ianuarie α. QED.

Proprietățile liniilor perpendiculare și avioane:

1. Prin orice punct al spațiului plan se extinde perpendicular pe o anumită linie.
2. Dacă două planuri a și b sunt perpendiculare pe linia a, atunci ele sunt paralele.
3. Dacă unul dintre cele două planuri paralele perpendiculare pe linia dreaptă, iar celălalt plan este perpendicular pe această linie.

Teorema: Prin orice punct din spațiu nu face parte din planul trece printr-o linie perpendiculară pe acest plan, și numai unul.

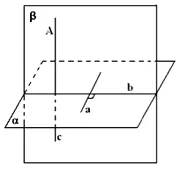
1. 1. Egal în planul a și linia arbitrară; construi planul β α, trece prin t A β α = β b în planul prin A trage o linie cu |. c α (c β și prin construcție cu ca β α). Deci, pentru a este linia dorită.
   2. Să ne dovedi că este singura. Să presupunem că acest lucru nu este cazul și există o alfa c1 directă, apoi un c1 ||. nu este posibil, deoarece c1 = A. Astfel, A trece printr-o singură linie cu planul α.

QED.