Teorema asupra echilibrului puterii și metoda de descompunere a forțelor în componente
mecanicii teoretice
Teorema asupra echilibrului sistemului plan al trei forțe neparalele
Teorema echilibrului sistemului plan al trei forțe neparalele poate fi formulată după cum urmează: este necesar, dar nu suficient pentru linia de acțiune a acestor forțe echilibrul sistemului în plan a trei forțe neparalele se intersectează la un moment dat.
Să încercăm să dovedească această afirmație, și să explice de ce condițiile stabilite în teorema nu este suficientă pentru echilibrul sistemului de putere.
Să presupunem că trei forțe P. Q și F sunt cuprinse într-un singur plan, linia de acțiune a forțelor P și Q se intersectează într-un punct A.
Pe baza investigării III și IV axiome de transfer static forțele P și Q-a lungul liniilor de punct de acțiune A. Bazat pe paralelogramul axioma găsi o rezultantă a acestor forțe FΣ.
Ca rezultat, vom obține un sistem de două forțe - FΣ și F., care este echivalent cu sistemul original de trei forțe.
Dar, în conformitate cu Axiom III, un echilibru este posibilă numai în cazul în care FΣ forțele și F se află pe aceeași linie dreaptă și îndreptate în direcții opuse, ceea ce înseamnă că linia de acțiune a forței F. aparținând sistemului original de trei forțe, de asemenea, trebuie să treacă prin punctul A .
Acest lucru dovedește teorema.
Această teoremă indică doar starea necesară de echilibru, ceea ce nu este suficient, pentru că cele trei forțe pot converg la un singur punct, dar nu să fie în echilibru, dacă suma lor vectorială nu este zero.
Liniile de acțiune forță care se intersectează la un moment dat, numit convergente.
Descompunerea forță în două componente
Descompusă în putere constitutiv - este de a găsi un sistem de forțe, echivalentul a forței. În general, descompunerea forței sarcină în două componente are un număr infinit de soluții, ca și puterea - vectorul dimensiune.
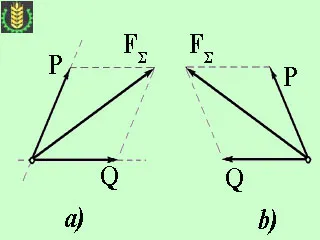
1. Există zone ale două componente P și Q (figura a).
În acest caz, direcția predeterminată a forțelor P și Q din punctul de aplicare al forței FΣ. atunci construim paralelogramul forțelor, luând vectorul forței FΣ diagonalei paralelogramului.
2. cunoscut magnitudinea și direcția de una dintre componentele.
metodă grafică soluție, ca și în primul caz se reduce la construirea paralelogramului; în care cunoscută magnitudinea și direcția uneia dintre laturile și diagonalelor paralelogramului (figura b).
3. Modulele cunoscute două componente P și Q (direcția nu este cunoscută).
Problema este rezolvată prin crestături, în care calibrată începutul vectorului forței FΣ realizat raza arc egal modulo un component (P sau Q) pe ambele părți FΣ vector. apoi de la sfârșitul vectorului a avut loc FΣ raza arcului de al doilea component pe ambele părți FΣ vector. arce punctele de trecere sunt vârfurile unui paralelogram de forțe dorite.
Problema în acest caz poate fi:
4. componenta direcție cunoscută și componenta Q a doua unitate P. Problema este rezolvată prin metoda serif. Astfel, de la începutul vectorului este efectuat line FΣ în direcția componentei vectorului a forței, și apoi prin capătul vectorului se realizează linia FΣ paralelă cu prima linie. Mai mult, de la începutul celei de a doua linie de vector FΣ făcut arc serifs a cărui rază este egală cu cea de a doua cunoscut modul component.
Sarcina poate fi:
- o singură soluție în cazul în care distanța dintre liniile paralele construite egală cu lungimea componentei forței formează un modul (în acest caz, unghiul dintre vectorii P și Q este egal cu 90 de grade);
- două soluții, dacă distanța dintre liniile paralele este mai mică decât lungimea componentei cunoscute a modulului forței;
- nu au soluții, dacă distanța dintre liniile paralele este mai mare decât modulul cunoscut componentă de forță.