Societatea fizică și matematică în liceu - cu soluția problemei

Probleme cu decizia. Oscilații și Valuri

1) La o sarcină orizontală netedă este conectat printr-un arc pentru un perete. Frecvența oscilațiilor ω naturale. Cargo a respins din poziția de echilibru la dreapta la L și eliberat. După o deviație de la poziția de echilibru, sarcina atinge l / 2. Care este viteza sa în acest moment. când accelerația este g.

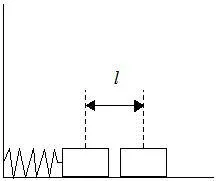
1) Înlocuind condițiile inițiale

2) Expresia pentru accelerația oscilație este:

Deoarece prin ipoteză. a = g.

Pentru rata avem:

2) Kubik pendulează cu o perioadă de 1 secundă într-un plan vertical a unei cești sferice, raza interioară, care este mult mai mare decât marginea cub. Bowl în repaus față de Pământ. Ce accelerare față de Pământ, și în ce direcție trebuie să se deplaseze castron vertical într-o matriță de timp de 1,5 min, 60 face oscilație.
Decizie.
Fluctuațiile cub oscilații echivalente ale unui pendul matematic. Într-adevăr, odată ce mișcarea cubului pe suprafața interioară a vasului sferic are loc fără frecare oscilații ale cubului, marginea care este mult mai mică decât raza cupei poate fi înlocuită cu oscilații ale corpului, dimensiunile geometrice ale care sunt mult mai mici decât lungimea firului pe care este spânzurat, punctul de suspensie este în centrul geometric castron sferic, iar lungimea firelor egală cu raza castron.

Potrivit problemei, în timp ce cupa se sprijină față de Pământ, perioada de oscilație T 0 este cub. o forță de tensionare a firului raportat la accelerație echilibru accelerație egală modulo cub de cădere liberă și îndreptat vertical în sus. atunci

unde R - lungimea firului egală cu raza suprafeței sferice a paharului.

Atunci când o accelerație verticală în raport cu pământ în mișcare forțele de tensiune fire cupa cubică stare de echilibru accelerare g ± a. în care semnul plus corespunde accelerării îndreptate în sus, iar semnul minus - accelerație îndreptate în jos. Să presupunem că pentru definiteness

De la expresii (1) și (2) vom găsi raportul dintre perioadele:

Analiza arată rezultatul rezolvării problemei că direcția de deplasare pe verticală a vasului (adică direcția vitezei sale) pentru perioada de oscilație a cubului nu este afectat. Este important să se cunoască direcția accelerației.

În acest caz, accelerarea direcției în jos a vasului, și este posibil, fie la scăderea accelerată a bolului sau în timpul creștere lentă. aceeași accelerație Modulul este

3) Plutitorul Densitatea lichidului ρzh înălțimea cilindrului h. În cazul în care butelia este cufundat adânc în lichid sau, în mod alternativ, scoate un pic de lichid, după ce a fost eliberat, cilindrul începe să oscileze. Densitatea materialului din care este confecționat cilindru, pM. Definiți frecvența de oscilație a cilindrului.

Starea corpului de înot: forța lui Arhimede egală cu forța de gravitație:

unde S - aria secțiunii transversale a cilindrului, x 0 - adâncimea ei de imersiune.

Definim adâncimea de scufundare a cilindrului:

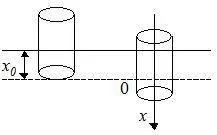
Dacă crește adâncimea de scufundare a cilindrului, forța de gravitație nu va compensa flotabilitatea și legea fundamentală a dinamicii pentru cilindru (în proiecția pe direcția axei x. De-a lungul care apar vibratiile) va arata ca

unde x - deplasarea cilindrului în raport cu poziția de echilibru, sau

Accelerație oscilații armonice variază conform formulei. Comparativ cu (1), pentru a obține frecvența naturală de oscilație

4) este coloana lungimea I a fluidului în tubul U formă. Pentru schimbări scurte presiunea fluidului într-un genunchi nivelurile de lichid mutat și coloana a început să fluctueze. Pentru a determina frecvența de oscilație. frecare de perete neglijat.

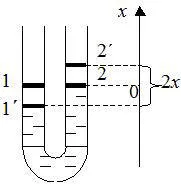
Prin deplasarea barei pe X în creșterea nivelului genunchiului drept de x. iar în stânga cade la -x (fluid incompresibil). mișcare fluidă va avea loc sub acțiunea forțelor de presiune:

unde S - aria secțiunii transversale a tubului, P - presiune.

În conformitate cu a doua lege a lui Newton

unde m - masa de lichid. Semnul minus este luată pentru că forța de presiune este îndreptată în direcția opusă deplasării. Prin urmare,

Comparând formula c pentru accelerare. Obținem pentru ω

5) La o rigiditate arc liber agățat la masa m sarcină atașat și eliberat. Oscilațiile mor încet. Găsiți: 1) deformarea maximă a arcului; 2) de energie încorporat în organism, după vibrațiile încetează complet.
soluţie:
Poziția de echilibru a masa m în primăvară va fi mai mic de x0 poziția inițială a masei :. Deoarece vibrațiile sunt amortizate lent în prima sarcină jumătate de ciclu scade sub x0 poziție de echilibru, de asemenea, practic (amplitudinea inițială). Cu alte cuvinte, deformarea maximă a arcului va fi
.
Energia încorporată în organism, găsim legea conservării energiei. În starea inițială a sarcinii de sistem are un potențial energetic. Această energie (starea finală) sa mutat în energie de deformare de primăvară și căldură Q:

de atunci

1,443,955 de vizitatori unici