sistem compatibil de ecuații liniare

ecuație algebra vector matrice

Având în vedere un sistem de ecuații liniare. Dovedește-l împreună și de a rezolva în două moduri:

a) metoda lui Cramer;

b) prin intermediul calculului matricei.

Vom examina compatibilitatea sistemului:

Noi folosim Teorema lui Kronecker-Capelli, pentru aceasta vom găsi rangul matricei augmentată a sistemului și rangul matricei sistemului.

Aici am crescut matrice sistem la eșalonul de formă prin transformări elementare, și definesc numărul de rânduri nenule în matrice.

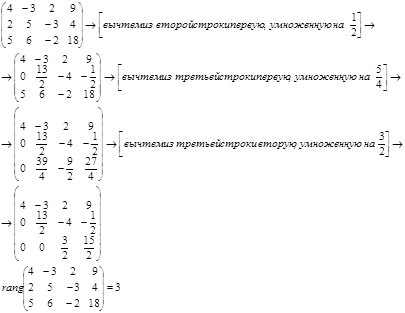
Lăsați matrice sistem să esalonului formă prin transformări elementare, și definesc numărul de rânduri nenule în matrice.

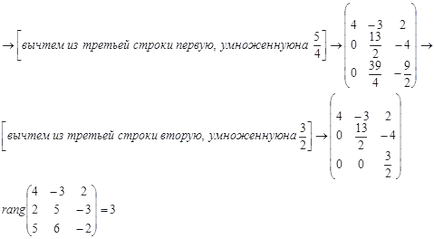
Deoarece rangul sistemului este egal cu rangul matricei augmented, atunci sistemul este consistent.

Să ne găsim soluția sistemului prin regula lui Cramer:

Scriem matricea de bază a sistemului și pentru a găsi determinantul său:

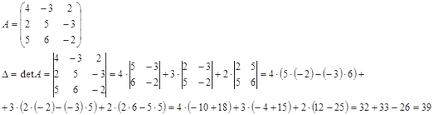
Ca sistem de matrice principal definițională (principalul determinant) nu este zero, sistemul este o articulație.

Substitut deciziile coloanei în prima coloană a matricei principal și să determinantul său:

Vom înlocui o coloană de decizii în a doua coloană a matricei principal și să determinantul său:

Membru supleant realizarea coloană în a treia coloană a matricei principal și să determinantul său:

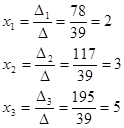
Să ne găsim soluția mod matricial:

Am găsit matricea inversă. Să ne găsim cofactori:

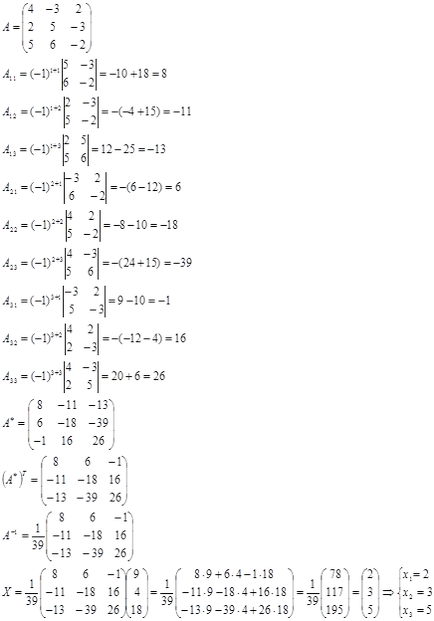
Având în vedere coordonatele de noduri ale unei piramide. Mijloace de algebră vectorului pentru a găsi:

2) unghiul dintre aripioarele și;

3) suprafața feței;

4) Volumul piramidei;

Am găsit A1 A2 lungimea muchiei cu formula

Unghiul b între marginile A1 A2 A1 A4 și egal cu unghiul dintre vectorii și. Am găsit coordonatele acestor vectori:

Apoi unghiul b determinat din raportul

3) Găsiți produsul vectorial

Apoi zona feței A1 A2 A3 este

4) Găsiți produsul mixt

Apoi, volumul piramidei:

Demonstrați că vectorii sunt liniar independente, și pentru a găsi extinderea vectorului în baza vectorilor.

Noi forma matricea coordonatelor vectorilor și determină rangul. Pentru a face acest lucru, vom reduce la o formă triunghiulară.

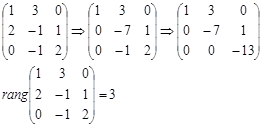
sistem de vector Locul este 3. Vectorii sunt liniar independente și trei dintre ele și pentru că acestea sunt de trei-dimensionale, ele formează o bază în spațiul tridimensional. Orice spațiu vectorial poate fi extins în vectorii acestui sistem.

Noi găsim coordonatele de descompunere. Noi înlocui coordonatele vectorilor în ultima egalitate.

Deoarece vectorii sunt egale, atunci coordonatele lor sunt egale.

Un sistem de trei ecuații liniare cu trei necunoscute. rezolva aceasta

Descompunerea vectorului (6, 12, -1), în această bază are forma

Având în vedere cele trei vârfuri ale triunghiului.

a) partea ecuație AB;

b) lungimea laturii soarelui;

c) înălțimea ecuației coborâtă de la un vârf A;

d) un sistem de inegalități care definesc triunghiul ABC.

a) parte a ecuației ca ecuația AB găsi o linie care trece prin două puncte:

b) Lungimea laturii BC descoperim distanța dintre B curent și C:

c) Înălțimea - linia care trece prin punctul A, perpendicular pe linia dreaptă BC. Să ne găsim ecuația liniei BC și vectorul de direcție:

Apoi, ecuația de înălțime:

g) instituie un sistem de inegalități liniare care definesc un triunghi. Pentru a determina semnul inegalității în partea stângă a fiecărei ecuații părți opuse coordonate de substituție ale nodurilor care aparțin semiplanul respectiv garantat.

Substituind punctul C (0, 5) în părți ecuație AB:

Substituind punctul B (18, 8) în partea AC:

Substituind punctul A (12, 0) în BC partea ecuația:

Deci, vom scrie sistemul necesar de inegalități:

L'Hôpital regula lui nu este de a găsi limitele de funcții.

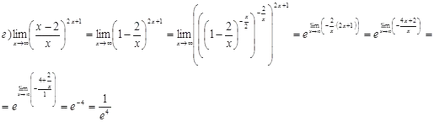
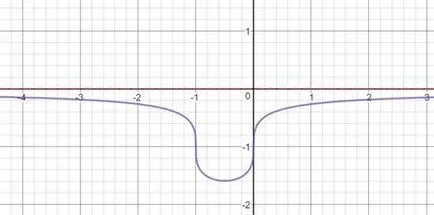
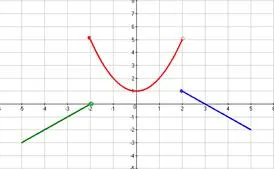
Găsiți puncte funcția de pauză, în cazul în care acestea există, funcția de salt la fiecare punct al diferenței și de a construi un program.

Domeniul de porțiuni - este unirea tuturor componentelor sale. Astfel,

Este evident că toate cele trei funcții sunt continue la intervale corespunzătoare, astfel încât vom verifica punctele de frontieră.

Noi investigăm punctul x continuitate = -2

- Funcția este definită la punctul dat

Am găsit limitele unei fețe:

Limitele sunt finite și unilaterale distincte, atunci funcția f (x) are un prim ordin de discontinuitate cu salt în punctul x = -2.

Calculeaza o discontinuitate salt ca diferență între limitele dreapta și din stânga:

și anume grafic a crescut până la 5 unități.

Pentru a investiga continuitatea punctului x = 2.

- Funcția este definită la punctul dat

Am găsit limitele unei fețe:

Limitele sunt finite și unilaterale distincte, atunci funcția f (x) are un prim ordin de discontinuitate cu salt în punctul x = 2.

Calculeaza o discontinuitate salt ca diferență între limitele dreapta și din stânga:

și anume Programul se duce în jos 4 unități.

Asimptotă acolo. Există două tipuri de prim discontinuitate la x = -2, cu un salt egal cu 5 și x = 2, cu un salt egal cu -4.

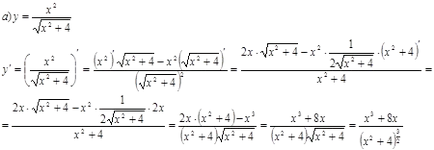
Găsiți derivatele acestor funcții.

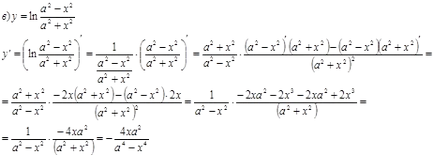
Găsiți raza de bază și înălțimea cel mai mic volum al conului circumscris despre raza R. mingii

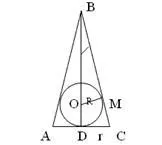
Figura secțiune axială prin con.

ABC - triunghi isoscel AB = BC;

Despre - centrul cercului inscris;

M - punctul de contact cu circumferința BC lateral;

D - punctul de tangență cu okuzhnostyu bază triunghi.

Lăsați înălțimea conului este egală cu x, apoi din triunghiul OBM (dreptunghiular)

Triunghiuri VSD și PTO sunt similare în cele două colțuri, atunci egalitatea:

Găsim volumul unui con:

Noi investigăm funcția V (x) al extremelor:

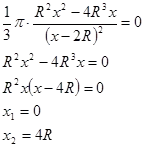
Considerăm că un punct x = 4R este un punct minim. Prin urmare, cel mai mic volum al înălțimii conului este h = 4R

Raza de cel mai mic volum al conului:

Exploreaza metode de calcul diferențial funcții și complot:

1) FIELD determinare

2) paritate, impar.

Verificăm se realizează dacă oricare dintre ecuațiile:

În acest caz, funcția va fi chiar

În acest caz, funcția va fi impar

Prin urmare, această funcție nu este nici măcar, nici ciudat. forma generală a funcției.

Concluzionăm că graficul funcției nu este simetrică în raport cu orice axă Oy. nici despre originea.

Această funcție nu este periodică.

4) Funcția de continuitate.

Întregul domeniu al acestei funcții este continuă ca un polinom.

5) Punctele de intersecție cu axele

Punctele de intersecție cu Ox

Astfel, graficul funcției nu se intersectează axa Ox.

Punctele de intersecție cu axa y

Astfel intersecția este la punctul (0, -1)

6) funcționează în maniere se termină domeniu.

Capetele definiției câmpului sunt „- # 63,“ și „+“. Găsim limitele funcției la

Aceasta indică prezența unei asimptota y orizontală = 0.

5) Punctele critice ale funcției, intervalele de monotonie

Pentru a găsi extremele funcției, găsim derivatul și setați-o egală cu zero, rădăcinile acestei ecuații sunt punctele critice.

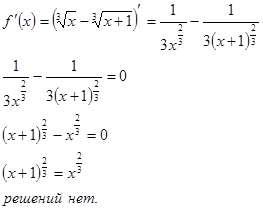
Nu există puncte de extremum.

6) Puncte de inflexiune, intervale de convexitate, concavitate

Noi găsim punctul de inflexiune. Pentru a face acest lucru, trebuie să găsiți derivata a doua a funcției și echivala-l la zero. Rădăcinile ecuației rezultată va fi punctul de inflexiune pentru graficul specificat funcției.

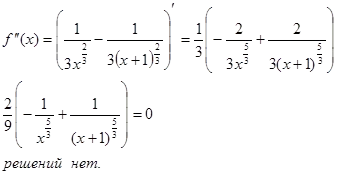
Nu există puncte de inflexiune.

7) Schița grafic