Simplificarea expresiilor logice

conversie Echivalent formule logice au aceeași funcție ca și formulele de conversie în algebra normală. Acestea servesc pentru a simplifica formulele, sau să le aducă la o anumită formă prin folosirea legilor de bază ale algebra logicii.

Sub Formula realiza conversia simplificare echivalentă, rezultând într-o formulă care nu conține nici una dintre operațiile de implicare și disjuncției strictă echivalență sau conține în comparație cu numărul minim inițial al operațiunilor de conjuncție, disjuncție și inversiuni sau conține un număr minim de variabile.

Unele transformări ale formulelor logice similare cu formulele de conversie în algebra obișnuită (impunerea unui factor comun din paranteze, folosesc legile comutative și asociative, etc.), în timp ce altele se bazează pe transformarea proprietăților care nu le posedă operații obișnuite de algebră (folosind legea distributiv pentru conjuncțiilor , legile de absorbție, lipire, de Morgan și colab.).

Vom arăta câteva exemple în tehnicile și metodele utilizate în simplificarea formulelor logice.

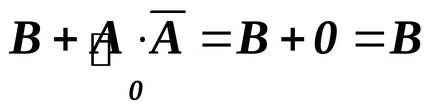
În acest exemplu, aplicat legile contradicție (11) și constantele de excludere (7).

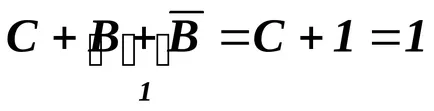
În acest exemplu, principiul aplicat contradicției (11) și operația definiție „adăugarea logică“.

În exemplul 3 Aplicând legea contradicției (11) și constantele de excludere (7).

În exemplul (4) legea contradicției (11) și operația definiție „ANDing“ aplicată.

Legile Boolean se aplică în acest exemplu, în următoarea ordine: regula DeMorgan lui (14), legea asociativă (6), legea contradicției (11) și operațiile de regulă cu constante (7).

Legile Boolean în acest exemplu este utilizat în această ordine: regula de Morgan (14) este scos din paranteze factorul comun (distributivitate (8)), legea contradicției (11).

În acest exemplu, negative pentru regula formulele nonelementary se aplică De Morgan ((14) și (15)); legea asociativă (6) se utilizează legi duble negativ (13) iar operația definiție „plus logică“.

De multe ori, pentru a simplifica expresii booleene se aplică următoarele identități:

Folosind aceste formule înseamnă că orice expresie poate fi multiplicată cu unitatea sau adăuga orice cuvinte de zero. exemplu:

Aceste exemple arată că simplificarea formulelor logice nu este întotdeauna evidentă, care a legilor algebra logicii ar trebui aplicate la un anumit pas. Abilitati vin cu experienta.

Construcția funcțiilor logice, bazate pe expresii matematice

funcțiile logice sunt adesea formate pe baza unor expresii matematice. Expresia matematică este cunoscută pentru a conține variabile, constante și funcții legate de semne de operații matematice. Dar, pentru a crea o funcție logică necesară pentru a utiliza operatori relaționale: <,>, ≤, ≥, =, ≠. Rezultatul oricăreia dintre aceste operațiuni este „adevărat“ sau „fals“, pe care o vom nota 1 sau 0. Astfel, fiecare relație operațiune creează o declarație simplă.

De exemplu, expresia X> Y este 0 sau 1, în funcție de valorile particulare ale lui X și Y. Astfel, este posibil să se formeze o funcție logică f variabilelor reale X și Y, care va fi valabil dacă este îndeplinită condiția definită mai sus. Este scris ca aceasta:

Un alt exemplu. Forma o funcție logică, care va fi adevărat în cazul în care variabilele x și y sunt multipli de trei; x, variabile întregi y-.

Decizie. Rețineți că un număr întreg și este un multiplu al unui număr întreg b. în cazul în care restul împărțirii întreagă a lui b este zero:

Aici, operația de înregistrare mod înseamnă calcularea unui reziduu atunci când diviziune întreagă a lui b.

Condițiile problemei este ușor de identificat două declarații simple: x este un multiplu de trei și y este un multiplu de trei. Între aceste afirmații ar trebui cuvântul „și“. Prin urmare, aceasta este o propunere dificil conține multiplicare logică, și matematic această afirmație poate fi scrisă ca:

Luați în considerare un alt exemplu. Forma o funcție logică, care va fi valabil în cazul în care suma a și b- pozitiv, în timp ce valoarea unui sau b- negativ. și b- un tip de variabile reale.

Decizie. În acest exemplu, câteva afirmații simple pot fi de asemenea identificate:

Valoarea a- este negativă;

Primul citat este asociat cu alte doua uniune „o“, ceea ce înseamnă că între multiplicarea logică. Mai mult, declarații simple doua și a treia conectate prin „sau“, ceea ce înseamnă că între operația logică plus. Astfel, obținem următoarea funcție:

Parantezele în această expresie modifica ordinea operațiilor. Acest lucru este necesar deoarece operatorii relaționale au cea mai mică prioritate.

O altă clasă de operațiuni de relații asociate cu planul de coordonate. Să ne dea un exemplu simplu, pentru a forma o funcție logică, care va fi adevărat în cazul în care punctul aparține zonei umbrite (a se vedea figura 1.).

Decizie. Conform figurii, punctul ar trebui să fie în interiorul cercului de rază 1 cu o singură mână, iar pe de altă parte - să fie în jumătatea superioară. Ecuația cercului de rază 1 are forma:

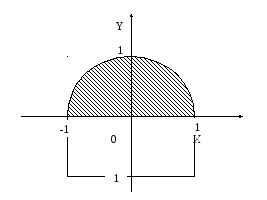
în care X și Y - coordonatele punctelor care aparțin cercului. Ideea este în interiorul cercului dacă coordonatele sale îndeplinesc condiția următoare:

Până la un punct în jumătatea superioară a fost condiția necesară Y ≥ 0. Aceste două condiții trebuie îndeplinite simultan, ceea ce este posibil numai pentru multiplicare logică. Astfel, funcția necesară este de forma: