Al doilea semn al funcțiilor extreme
în cazul în care, apoi - punctul maxim.
După cum puteți vedea, această caracteristică necesită existența unui extremum de derivat de funcții cel puțin până la a doua comanda la punctul.
Găsiți extremele funcției.
Să începem cu definiția câmpului:
Ne diferentiem funcția originală:

Derivatul devine zero, atunci când x = 1. că este, acesta este punctul de extremum unei posibile. Suntem un al doilea derivat al funcției și calcula valoarea la x = 1.
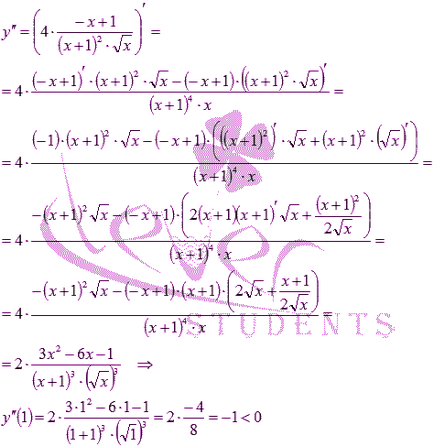
Prin urmare, în conformitate cu a doua condiție suficientă pentru extremum, x = 1 - punctul maxim. Apoi, - funcția maximă.
A treia condiție, suficientă pentru funcții extreme.
Lăsați funcția y = f (x) are derivați de n-lea ordin în vecinătatea punctului și derivatele n + 1 th ordine la punctul. Să.
în cazul în care n - chiar și atunci - punctul de inflexiune;
în cazul în care n - ciudat, apoi - un punct extrem, și
în cazul în care, apoi - punctul minim;
în cazul în care, apoi - punctul maxim.
Găsiți punctul de funcții extreme.
Funcția original este un întreg rațional, domeniul său este întregul set de numere reale.
Derivata dispare în consecință, posibil punct de extremum. Noi folosim al treilea extremum suficient.
Suntem un al doilea derivat și calculează valoarea la punctele posibile extremum (calcule intermediare omise):

Prin urmare, - punctul de maxim (pentru al treilea criteriu extremum suficient au, și n = 1).
Pentru a elucida natura celui de al treilea derivat găsi puncte și calcula valoarea la aceste puncte:

Prin urmare, - punctul de inflexiune al funcției (n = 2 u).
Rămâne să se ocupe cu punctul. Am găsit un sfert derivat și se calculează valoarea sa în acest moment:

În consecință, - punctul de minim al funcției.

- înalt punct - punctul de minim al funcției.
10. Determinarea extremelor funcției
Funcția y = f (x) se numește creștere (descreștere) un anumit interval de timp, în cazul în care x1
Dacă funcția diferențiabilă y = f (x) în intervalul [a, b] crește (descrește), atunci f „(x) derivat în acest interval 0
punctul Ho se numește un maxim local (minim) al funcției f (x), în cazul în care există o vecinătate Ho. pentru toate punctele unde inegalitatea f (x) ≤ f (Ho) (f (x) ≥ f (Ho)).
Punctul maxim și minim de puncte sunt numite extreme. și valorile funcției de la aceste puncte - extremele ei.
punctul extremum
Condițiile necesare pentru un extremum. Dacă Ho este un extremum punct al funcției f (x), atunci fie f „(Ho) = 0 sau f (Ho) nu există. Aceste puncte sunt numite critice, iar funcția este determinată la punctul critic. Extremele funcții se găsesc printre punctele sale critice.
Prima condiție este suficientă. Să Ho - un punct critic. Dacă f „(x) atunci când trece prin punctul Ho schimbă semnul de la plus la minus, apoi la punctul de funcția Ho are un maxim, în caz contrar - cel puțin. Dacă trec prin punctul critic al derivatului nu se schimbă semnul, apoi la punctul Ho nu este extremelor.
A doua condiție suficientă. Să presupunem că funcția f (x) este f derivat „(x) într-un cartier al Ho și al doilea derivat de la punctul Ho. Dacă f „(Ho) = 0,> 0 (<0), то точка xо является точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.
Pe intervalul [a, b] funcția y = f (x) poate ajunge la cea mai mică sau cea mai mare valoare sau punctele critice sau segmentele de la capete [a, b].
Exemplul 3.22. Găsiți extremelor funcției f (x) = 2x 3 - 15x 2 + 36x - 14.
Decizie. Deoarece f „(x) = 6x 2 - 30x +36 = 6 (x -2) (x - 3), punctele critice ale 2 și x1 = x2 = 3. extremele poate fi doar la aceste puncte. Deci, pe măsură ce trece prin punctul x1 = 2 modificări derivate semn de la plus la minus, apoi la acest punct funcția are un maxim. La trecerea prin punctul x2 = 3 modificări derivate semn de la minus la plus, astfel încât la punctul x2 = 3 pentru funcția de cel puțin. Calcularea valorilor funcției la punctele x1 = x2 = 2 și 3, găsim extremele funcției: maxim de f (2) = 14 și minimum f (3) = 13.