sarcini B9

Vom continua tutorial №8 examen la matematică.
Astăzi, avem nevoie de tabelul de mai jos pentru a rezolva problemele. arată relația semnului derivat cu funcție monotonă.
Vă rugăm să fie extrem de atent în următoarea. A se vedea programa CE dat la tine! Funcția sau derivatul său
În cazul dat graficul derivatului. care ne interesează sunt doar semne ale funcțiilor și zerouri. Nu există „dealuri“ și „depresie“ nu ne interesează în principiu!
Figura prezintă o diagramă a unei funcții definite pe intervalul. Se determină numărul de puncte zabrele, în care derivatul este negativ.
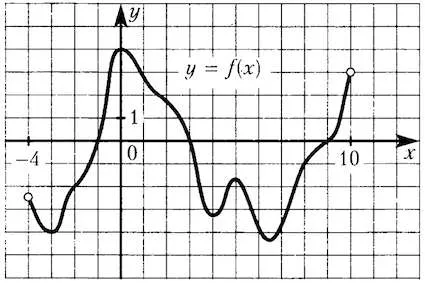
În figura sunt evidențiate funcție de zona descrescătoare:
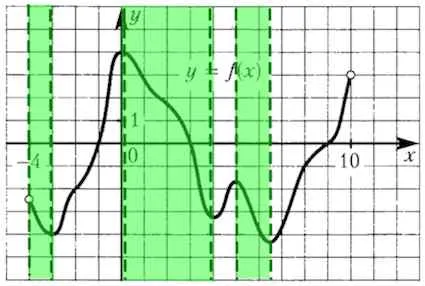
În aceste zone scădere a funcției scade 4 valori întregi.
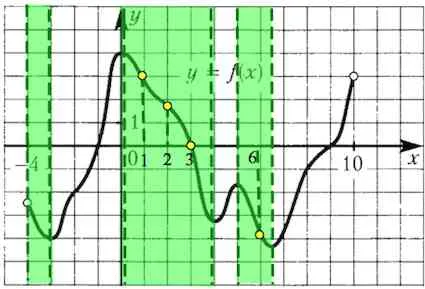
Figura prezintă o diagramă a unei funcții definite pe intervalul. Găsiți numărul de puncte la care tangenta la graficul de drepte paralele sau coincid cu ea.
Odată tangenta la graficul paralel (sau coincide cu) linia (sau, echivalent,) având o pantă egală cu zero, iar panta tangentei are.
Aceasta înseamnă că tangenta este paralelă cu axa, deoarece panta este panta tangentei la axa.
Prin urmare, găsim în punctul graficul extremelor (puncte maxime și minime), - în care tangenta la graficul funcției să fie paralelă cu axa.
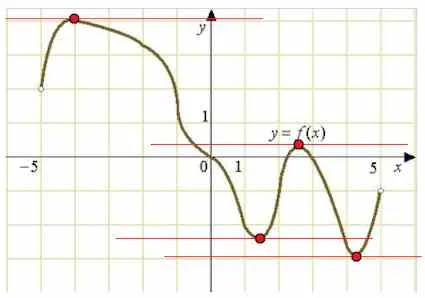
Figura prezintă un grafic al funcției derivatului definit pe intervalul. Găsiți numărul de puncte la care tangenta la graficul de drepte paralele sau coincid cu ea.
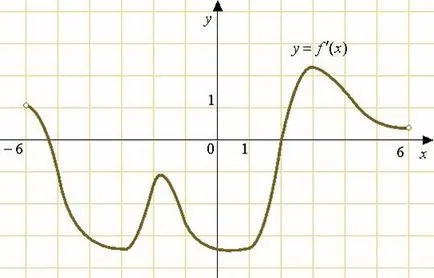
Odată tangenta la graficul paralel (sau meci), linia dreaptă având o pantă, iar panta tangentei are.
Aceasta, la rândul său, înseamnă că punctele de contact.
Prin urmare, uita-te cat mai multe puncte de pe grafic sunt ordonata egale.
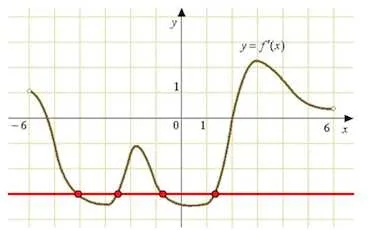
După cum puteți vedea, aceste puncte - patru.
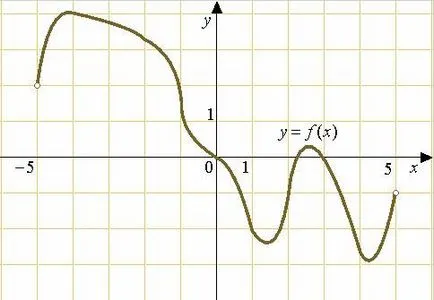
Figura prezintă o diagramă a unei funcții definite pe intervalul. Găsiți numărul de puncte la care derivatul este 0.
Derivatul este zero la punctele extremum. Noi le avem 4:
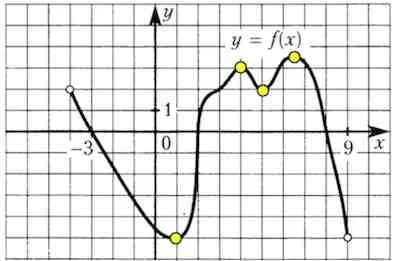
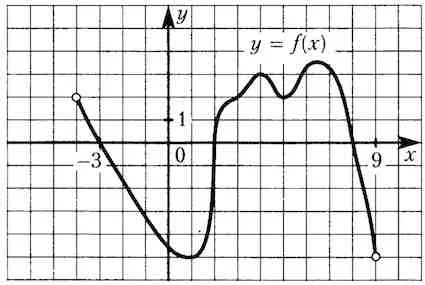
Cifra reprezintă un grafic al funcției și unsprezece puncte pe axa x. În cât de multe dintre aceste puncte derivata negativ?
La intervale de scădere derivata funcției este negativ. O scădere de puncte funcționale. 4 astfel de puncte.
Figura prezintă o diagramă a unei funcții definite pe intervalul. Găsiți suma punctelor de funcții extreme.
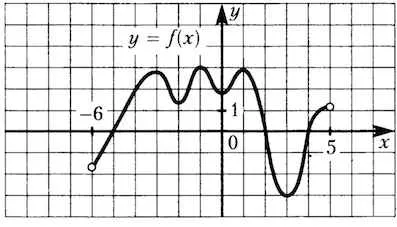
Punctele extremum - punctul maxim este (-3, -1, 1) și punctul minim (-2, 0, 3).
Puncte Suma extremum: + 1-2 + -3-1 0 + 3 = -2.
Figura prezintă un grafic al funcției derivatului definit pe intervalul. Găsiți intervalele de creștere a funcției. Ca răspuns, specificați cantitatea de puncte Lattice incluse în aceste intervale.

Cifra marcat spații pe care este derivat pozitiv.
Pe mic decalaj crește puncte zabrele acolo, diferența crește patru valori întregi, și.
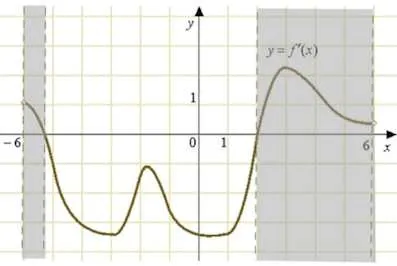
Figura prezintă un grafic al funcției derivatului definit pe intervalul. Găsiți intervalele de creștere a funcției. În răspunsul dvs., lungimea cea mai lungă dintre ele.
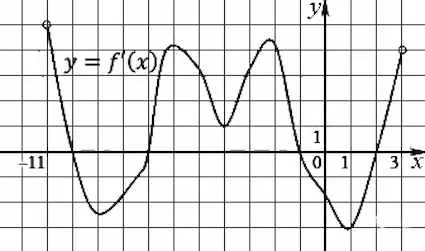
În figură sunt evidențiate toate spațiile pe care derivatul este pozitiv, și, prin urmare, funcția în sine crește în aceste intervale.
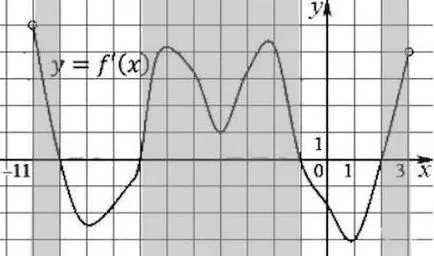
Lungimea cea mai lungă dintre ele - 6.
Figura prezintă un grafic al funcției derivatului. definite pe intervalul. La un moment dat, în intervalul are cea mai mare valoare.
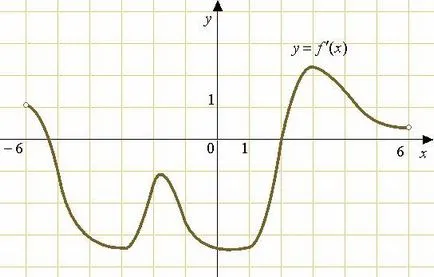
Uita-te la comportamentul grafic pe intervalul, și anume, ne interesează doar semnul derivatului.
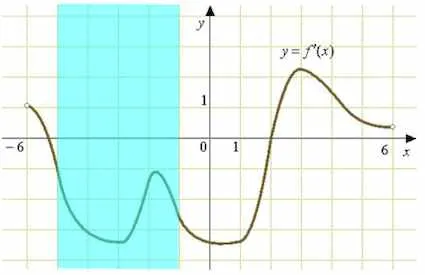
Semnul derivatului de - negativ, ca un grafic pe acest segment sub axa.
Aceasta înseamnă scăderea funcției pe intervalul.
Deci, cea mai importantă funcție durează de la începutul segmentului, care este punctul.
Sarcina 10.
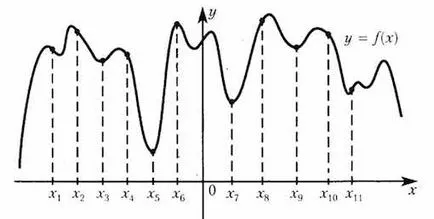
Figura prezintă un grafic - funcția derivat definit pe intervalul. Găsiți numărul de puncte maxime ale funcției în intervalul.
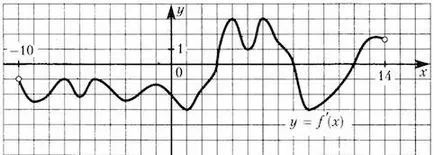
Figura prezintă graficul derivatului, așa că trebuie să dăm această voință interes doar semnele și zerouri ale derivatului.
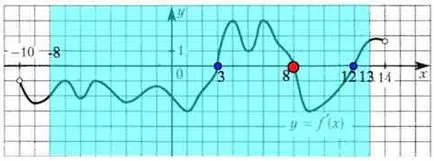
Ne vedem în imagine la un anumit interval () trei zerouri de la. Mai mult decât atât, derivatul mnyaet semnul când trece prin el. Acesta este punctul de funcții extreme (puncte maxime și minime).
Când modificările derivate de la semn „+“ la „-“ la punctul 8, etichetate în roșu, și „-“ la „+“ în două puncte (3 și 12), marcată cu albastru.
Deci, atunci când trece prin punctul maxim al funcției de modificări privind creșterea scădere, și, prin urmare, modificările derivate semn de la „+“ la „-“.
Deci, punctul de maxim o (marcate cu roșu).
Sarcina 11.
Figura prezintă un grafic al funcției și punctul marcat -3, 1, 6, 8. În unele dintre aceste puncte este cea mai mică valoare a derivatului? Ca răspuns, specificați acest punct.
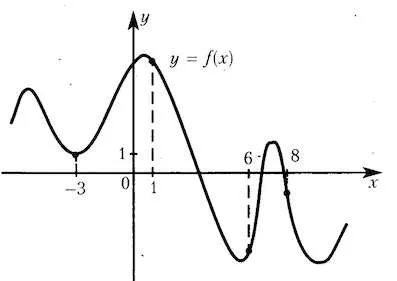
Valoarea derivatului de la punctul de contact este egal cu panta tangentei. La rândul său, panta tangentei este egală cu panta tangentei la axa.
La punctul 3 (punctul minim), derivatul este zero.
La punctul 6 derivatul este pozitiv, deoarece punctele se află funcția creșterea intervalului.
Dar, la punctele 1 și 8 din derivatul este negativ.
La acest punct 8 în unghiul de înclinare tangențială este în mod clar mai mic decât la punctul 1.
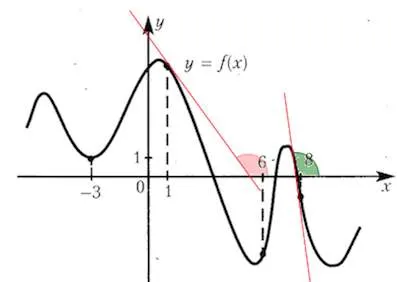
Prin urmare, la punctul 8, panta va fi cea mai mică, și astfel valoarea derivatului va fi cea mai mica.
) Este timpul să se relaxeze un pic. Nu-i așa? -> + spectacol
Nu a fost ușor.
Acesti tipi, probabil, nu sunt prea dulce ... Nu renunța!


Bună seara! Am o întrebare, de asemenea, a derivatului, dar se referă și Specta convexitate / concavitate. De ce functia y = x ^ 4 / (X ^ 3 + 1), punctul critic al doilea tip de parte la concavitate interval, acesta este un punct critic în al doilea derivat al său este egal cu 0, și am avut nevoie, conform teoremei iau doar intervale în care derivata a doua mai mare decât zero. Vă mulțumim anticipat pentru răspunsul dumneavoastră
Galina, după cum am înțeles, trebuie să se facă distincția între strictă și convexitate non-strictă / concavitatea ...
Elena, mulțumesc pentru răspunsul, din greșeală funcția greșit introdusă. De fapt, întrebarea mea este următoarea, eu sunt profesor și sunt interesat de modul matematic alfabetizare elevii mei boboci explica concavitate convexitate pentru functia y = x ^ 4, pentru că există un punct critic al doilea tip 0, pe baza cărora le explică faptul că funcția pe domeniul său este convex în jos, 0 piedica. Mulțumesc.
În sarcina 2 răspunsul nu este 3? Versantul este egal cu 0, atunci y = 0 intersectează funcția în trei puncte.
Dasha, în cazul în care graficul funcției f „(x) (și nu f (x)) a fost arătat în figură, atunci argumentul tău ar fi corect.
Comparați sarcini 2 și 3.
Pentru instrucțiuni 7 - De ce este x = nu include punctul 2? După - „Dacă funcția este continuă pe intervalul [a, b] și creșteri (scăderi) în intervalul (a, b), crește (scade), iar intervalul [a, b]“
Site-ul A. Larin EgeTrener - O. Sebedash Math Easy! CSE? Ok! - J. Feldman
