regula de faza Gibbs 1

starea sistemului, în care mai multe faze sunt în echilibru, se numește eterogen. Acest echilibru este posibil, dacă temperatura, presiunea și chimice potențialul fazelor sunt aceleași.

Lăsați sistemul include o componentă K, iar acest sistem este în A - faza, caz în care problema numărul de parametri independenți, care sunt necesare pentru o descriere lipsită de ambiguitate a sistemului, decide să se pronunțe că a primit Gibbs și care îi poartă numele.

Presupunem că sistemul nostru este sub presiune și temperatură constantă, în cazul în care starea de echilibru pentru fiecare fază poate fi scrisă ca:

unde $ F = H-TS = U + pV-TS $ - Gibbs energie (izobară - potențial izoterma), $ _I $ - potentialul chimic al componentelor cu număr i, $ n_i $ - componente de sistem - concentrare i. Numărul total de ecuații (1) egal cu numărul de faze Un total al acestor ecuații se numără $ (K \ cdot A) $ valori $ _I $, dar nu toate dintre ele sunt independente. Deoarece compoziția fiecărei faze nu se schimbă, atunci există o relație între potențialele chimice, respectiv, aceste condiții obligațiuni numai (A). Potențialele chimice ale fiecărei componente în toate fazele trebuie să fie aceeași, adică:

Pentru fiecare i este A-1 egalitate se obține pentru toate componentele K (A-1) condiție. Rezultă din cele de mai sus că numărul de independent $ _I $ este:

\ [K \ cdot A-A-K \ stânga (A-1 \ dreapta) = K-A \ \ stânga (3 \ dreapta). \]

Desigur, presiunea și temperatura sunt, de asemenea, parametri independenți. Se pare că numărul de parametri independenți ($ f $), care sunt necesare pentru a descrie în mod unic un sistem format dintr-o componentă K și depozitate în fazele A poate fi scrisă ca:

Să ne amintim că gazele ideale, am descris cu ajutorul a doi parametri, de exemplu, presiune și temperatură, iar volumul a găsit din ecuația de stare. Ecuația (4) se numește regula de faza Gibbs.

Situația când echilibrul sistemului este afectat nu numai parametrii externi, cum ar fi presiunea și temperatura, ca, de exemplu, câmpuri electrice, câmpuri magnetice etc. În acest caz, nu prezintă factori externi bude 2 ca în (4) și B (în cazul general), atunci expresia poate fi scrisă ca:

în care B - număr de parametri externi independenți.

Uneori, de exemplu, de multe ori face acest lucru în metalurgie atunci când se analizează presiunea poate fi considerată sisteme condensate constante, iar influența lui neglijare, în acest caz, se crede că regula faza Gibbs este scris:

Cu alte cuvinte, se poate spune că, dacă oricare dintre parametrii sistemului extern este fix, (de exemplu, starea p = const și T = const), se efectuează, în general, sub forma unei faze (6).

Expresiile (4), (5) și (6) arată că numărul de grade de libertate nu poate fi negativ, nu are nici o semnificație fizică. Deoarece $ f \ ge 0 $, atunci numărul fazelor sistemului existent satisface inegalitatea:

\ [A \ le K + 2 \ \ din stânga (7 \ dreapta). \]

Inegalitatea (7) înseamnă că numărul de faze care pot fi în echilibru unul cu celălalt nu poate depăși numărul de componente de mai mult de două. Această afirmație este o altă formulare a regulii de faza Gibbs.

Într-un sistem monocomponent, $ 1 \ le A \ le 3 $. Când $ A = 3, \ f = $ 0, acest lucru înseamnă că cele trei faze pot exista în echilibru substanță (de exemplu, gaz, lichid și solid), într-un singur stat, care se numește punct triplu.

regulă fază Gibbs

Potrivit lui Gibbs regula, se obține că, odată cu creșterea numărului de componente în sistem crește gradele de libertate, pe de altă parte, în cazul în care numărul de etape ale sistemului crește, scade numărul de variabile necesare.

regula faza Gibbs este utilizat în metalurgie, inginerie chimica, stiinta materialelor. Acesta vă permite să calculeze numărul de faze în sisteme multicomponente și numărul de grade de libertate termodinamice.

Dacă în multifazice reacții chimice sistem, este necesar să se ia în considerare numărul de ecuații chimice. Compoziția acestor ecuații se ecuații legate concentrațiile, ecuația de bilanț material. Ecuațiile suplimentare trebuie scăzută din partea dreaptă a ecuației (4) sau prin simpla luând în considerare numărul de componente. Utilizați $ K „= K-l $ în loc de K, unde $ l $ - numărul de ecuații suplimentare.

Sarcina: Determinați $ A, K \ \ i \ f $ pentru sisteme de fluide - ea perechi folosind regula de Gibbs. Cum se termodinamice diagramă arată starea unui astfel de sistem?

Deoarece condiția ca un lichid sistem și vaporii săi, numărul de faze disponibile - două. Acest lucru înseamnă că A = 2, sistemul este un component al K = 1. Apoi, în conformitate cu regula numărul ecuațiile Gibbs care descriu în mod unic starea sistemului va fi egal cu:

Valorile corespunzătoare de substituție, obținem:

Deoarece numărul de ecuații, care este necesară pentru a descrie sistemul este egal cu unu, apoi o diagramă termodinamic, de exemplu în axele (p, T) sistem component a doua faze este prezentată ca AA linie (faza de fluid diagrama de tranziție în abur Fig. 1).

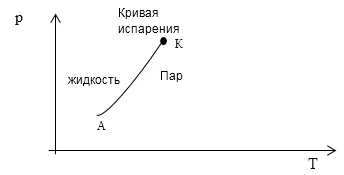
A: $ A = 2, \ K = 1 \ și \ f = 1 $. Starea de un astfel de sistem este prezentat în diagrama de fază a curbei din fig. 1.

Tema: Care este numărul de grade de libertate a unui sistem de stat cu trei faze cu o singură componentă. Ce se poate spune despre parametrii unui astfel de sistem într-o stare de echilibru?

Conform regulii de faza Gibbs, putem scrie:

Sistemul are un singur component: K = 1, un sistem cu trei faze, deci A = 3, numărul de ecuații de descoperire necesare pentru f regula Gibbs:

Realizăm substituirea datelor:

Raspuns: Deoarece $ f = 0 $, acest lucru înseamnă că cele trei faze ale unui sistem monocomponent poate fi în echilibru doar într-un singur raport de parametrii sistemului. Un astfel de punct este numit un triplu într-o diagramă termodinamic. Graficul la curbe triple punct de topire se intersectează, evaporare și sublimare.