Rata dobânzii dificilă

Rata dobânzii Complex compoundare - rata dobânzii la care baza de angajamente, spre deosebire de interes simplu, este n e r e m e n n o th. și anume se percepe dobanda pe interes.

După cum se prevede în prealabil o anumită perioadă de unități de acumulare de interes (an, lună, trimestru, etc), și rata dobânzii i (sau i% = 100 i). Lăsați suma inițială restantă este P. Apoi unitatea printr-un decalaj va fi suma taxei S 1 = P (1+ i), la fel ca în cazul simplu la sută. Cu toate acestea, până la sfârșitul total interval 2a unitate de lucru este S 2 = S 1 (1+ i) = P (1+ i) 2 (în contrast cu formula S 2 = P (1 + 2 i) pentru simplu la sută. Până la sfârșitul anului perioada 3 obține S 3 = S 2 (1+ i) = P (1+ i) 3. Și astfel sfârșitul perioadei unității n-lea obține

Deci, după n perioade de valoarea inițială a P va crește (1+ i) de n ori. Modificator (1+ i) n este numit factor de compoundare. Rețineți că, prin compusul acreție interes este o creștere a valorii inițiale a legii de progresie geometrică, care este primul termen și numitorul P. 1+ i.

Problema 1: Inițială suma depozitului P = 40.000 p. Rata dobânzii i% = 10% pe an. Determinarea naraschѐnnuyu la dobânda compusă timp de 3 ani și apoi se compară cu cantitatea de compunere schema de interes simplu.

Decizie. Aplicând formula (1), avem

S 3, complicat = P (1+ i) 3 = 40 000 (1 + 0,1) = 3 53 240 p.

Se calculează valoarea în cadrul schemei de interes naraschѐnnuyu simplu:

S 3, pr = P (1 + 3 i) = 40000 (1 + 0,3) = 52 000. <53 240 р.

Astfel, în acest caz, utilizarea rezultatelor compoundare într-o cantitate mai mare naraschѐnnoy că depunător avantajos comparativ cu schema de procente simplu incremental.

Formula de compunere de compoundare (1), derivată pentru întreaga

pozitiv n. aplicabile neîntreg t

Aici, P - suma inițială, n k - k perioadă de interes durata i k -lea și - rata dobânzii simple în perioada cu numărul k.

Sarcina 3. Contractul de servicii bancare de depozit timp de 4 ani, cu rată variabilă a dobânzii compuse fixe după cum urmează. În primul an - 6%, în anul 2 și 3, rata este aceeași - 5% pe an, pentru al 4-lea an

- 8%. Se determină valoarea unui factor de amestecare timp de 4 ani.

Decizie. Fie P - o anumită sumă inițială. Potrivit problemei

1 i = 0,06, i = 2 i 3 = 0,05, i 4 = 0,08.

Să i 23 = 0,05. Au în conformitate cu formula (2):

S = P (1, i 1) 1 (1 i 23) 2 (i 1 4) 1 = P (1 + 0,06) (1 + 0,05) 2 (1 + 0,08).

Ca rezultat al calculelor obținem valoarea factorului de amestecare:

S / P = (1 + 0,06) (1 + 0,05) 2 (1 + 0,08) = 1.262142.

Compararea creșterii simple și complexe la sută

În aceeași rată de interes i concreștere compoundare:

este mai rapid decât un interes simplu, în cazul în care durata perioadei de acumulare într-o singură perioadă;

Acesta este mai lent decât un interes simplu, în cazul în care durata perioadei de mai puțin de o singură perioadă de compoundare.

Anterior a fost observat că incrementul de bani pentru aceeași perioadă, indiferent dacă schema de procente simple sau complexe.

Să ne dovedesc cele de mai sus. De fapt, atunci când i> 0:

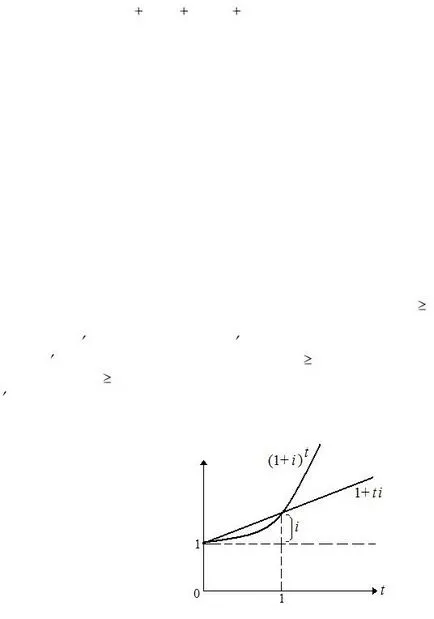
dacă t> 1, atunci (1+ i) t> 1+ l; dacă 0

Pentru a demonstra acest lucru, considerăm funcția f (t) = (1+ i) t și g (t) = 1+ l. Evident, f (0) = g (0), f (1) = g (1) și ambele funcții cresc la t 0 nu numai pentru un sens semnificativ, dar, de asemenea, în vederea pozitivitate formal derivate f (t) = (1+ i) t ln (1+ i) și g (t) = i. În același timp, derivata a doua comandă de f (t) = (1+ i) t 2 ln (1 + i) este pozitiv pentru t 0, ceea ce înseamnă că în jos funcția convexitate f (t) la t 0 (adică, o creștere accelerată) . Functia g (t) crește liniar

Graficul prezinta funcția f (t) = (1+ i) t și g (t) = 1 + l în funcție de t:

Exemplu. Să suma P = 800 este incrementat la rata i = 8% simple și complexe la sută. Apoi naraschѐnnye sumele sunt

Pentru a evalua perspectivele lor de creditori și debitori adesea importante pentru a ști cât de multe ori valoarea creditului este crescut de N ori la o rată a dobânzii dată i. Pentru a echivala acest factor agravând valoarea N., ca urmare a care obținem:

a) pentru simplu la suta 1 + ni = N. unde n = (N-1) / i.

b) pentru compoundarea (1 + i) n = N. unde n = ln N / ln (1 + i).

Problema 4. Se calculează numărul de ani datoria va crește la o rată a dobânzii de două ori mai simplu și compus de 4% pe an. Rezultatele sunt comparate.

Decizie. Prin problema condiție i = 0,04, N = 2. avem

a) interesul simplu pentru n = (N-1) / i = 1 / i. unde n = 1 / 0,04 = 25 ani

b) pentru compoundarea n = ln N / ln (1 + i), unde n = ln 2 / ln (1,04) 17,67 ani. Calculul sistemului de interes compus va dubla datoria.

Unele modalități de încărcare a dobânzii la un număr fracționar de ani

În practica instituțiilor financiare la un număr fracționar de ani t interes se calculează în mod diferit. Luați în considerare cele trei moduri principale de încărcare.

1. Prin formula compoundare: S = P (1+ i) t.

2. Pe baza metodei combinate conform căreia numărul întreg de ani de interes compoundare și pentru o fracționată - simplu: S = P (1+ i) n (1+ bi), unde t = n + b. n - un număr întreg s, b - partea fracționară a unui an.

3. O serie de bănci comerciale aplicate, în general, în conformitate cu durata de timp pentru care perioada mai mica de acumulare fără dobândă, adică

Problema 5. Dimensiunea creditelor acordate de 27 de luni este de 100 000. Rata anuală a dobânzii este de 20%. Se calculează Sumele naraschѐnnuyu exprimate în trei moduri.

Decizie. Potrivit problema perioada de creditare este de 2,25 ani. Avem următoarele calcule.

Conform metodei 1: S I = 100 000 (1 + 0,2) 2. 2 5 150 715 pe p. 46 copeici. Conform metodei 2a: S II = 100 000 (1 + 0,2) 2 (1 + 0,25 0,2) = 151 200 p. Pe treia metodă: S III = 100 000 (1 + 0,2) 2 = 144 000 p.

Formula scontarea când compoundare

În formula matematică a scontarea

În cazul în care actualizarea se efectuează în conformitate cu schema de contabilitate bancare (comerciale), The negociat inițial rata de actualizare d. d 0 <1. Она применяется не к начальной сумме, как при простой учетной ставке, а к сумме, уже дисконтированной на предыдущем промежутке времени. Размер дисконта, или учета, удерживаемого финансовым учреждением, равен

Sarcina 7. Un instrument pentru suma de 20 000 p. plata pe termen lung a care are loc în 1,5 ani, a reprezentat rata dobânzii compus de 18% pe an. Se determină suma primită de la proprietarul înregistrat al proiectului de lege, precum și reducerea corespunzătoare.

Decizie. Aici, cu condiția sarcini S = 20 000, n = 1,5, d = 0,18. Apoi, cu formula (4), obținem următoarele rezultate de calcul:

suma primită de către proprietarul P = 20.000 (1 - 0.18) 1.5 14850 p. 83 copeici.

discount D = S - P 20 000 - 5149 = p 14850.83. 17 copeici.