rădăcinile raționale ale unui polinom cu coeficienți întregi
Problema găsirii f (x) rădăcini raționale polinomiale
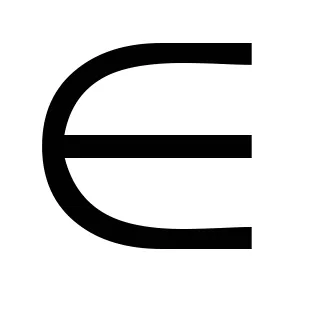
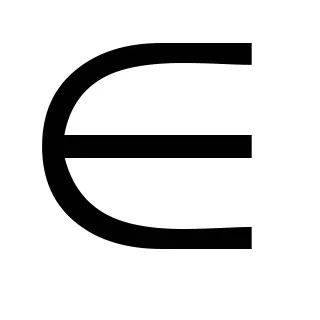
condiții suficiente necesare, dar nu și pentru existența unor rădăcini raționale ale unui polinom cu coeficienți întregi date de următoarea teoremă.
Teorema 6.1 (pe rădăcinile raționale ale unui polinom cu coeficienți întregi) .Dacă
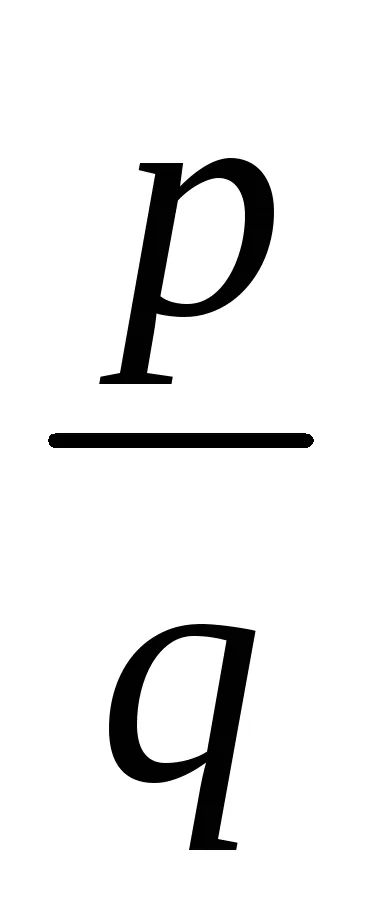
teorema 6.2.Esli
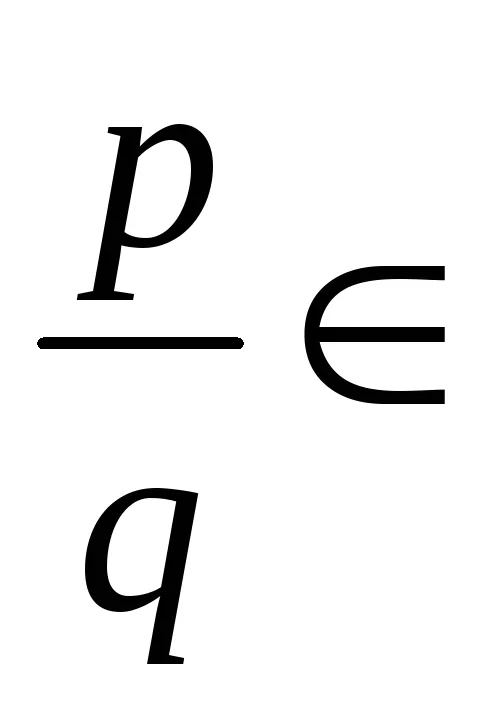
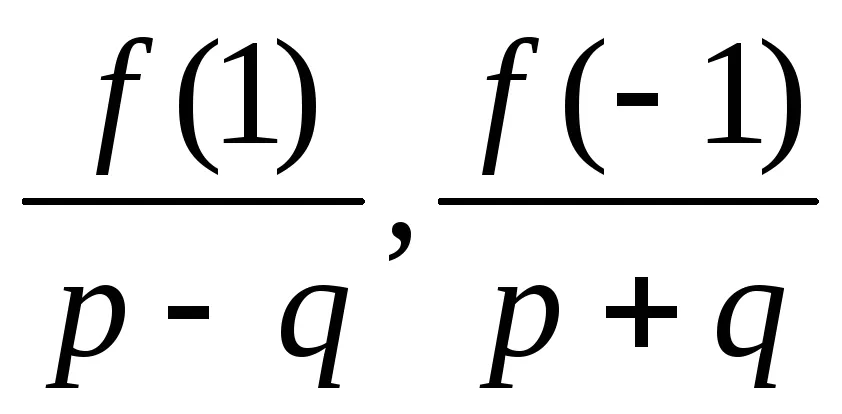
Exemplu. Găsește toate rădăcinile raționale ale polinomului
1. Prin Teorema 6.1: dacă
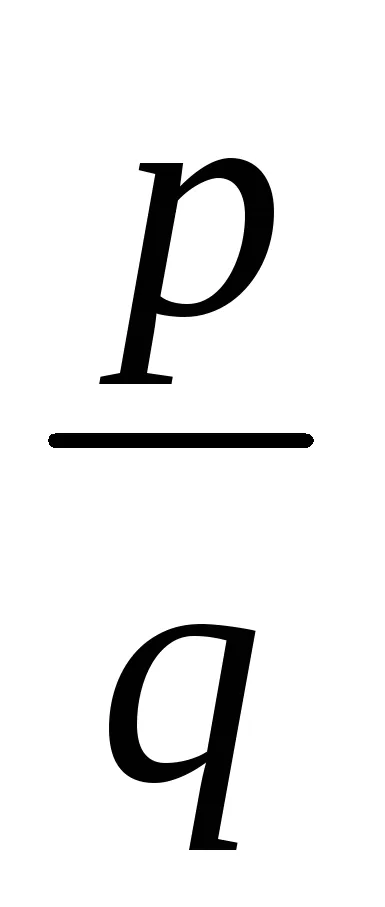


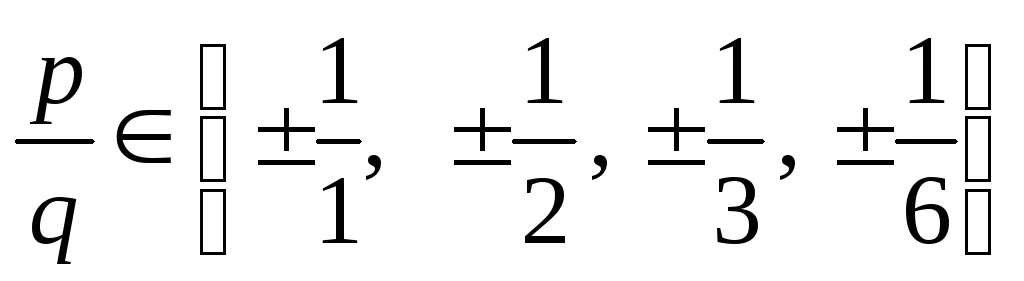
2. Este cunoscut faptul că (corolarul 5.3), numărul a este o rădăcină a f polinomului (x) dacă și numai dacă f (x) este împărțit la (x - a).
Prin urmare, pentru a verifica dacă numerele 1 și -1 rădăcinile f polinomului (x) se poate utiliza schema Horner:
Primit: q (
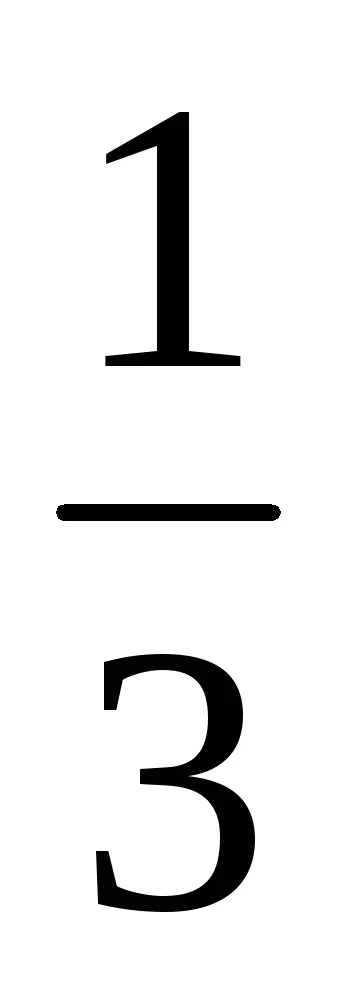
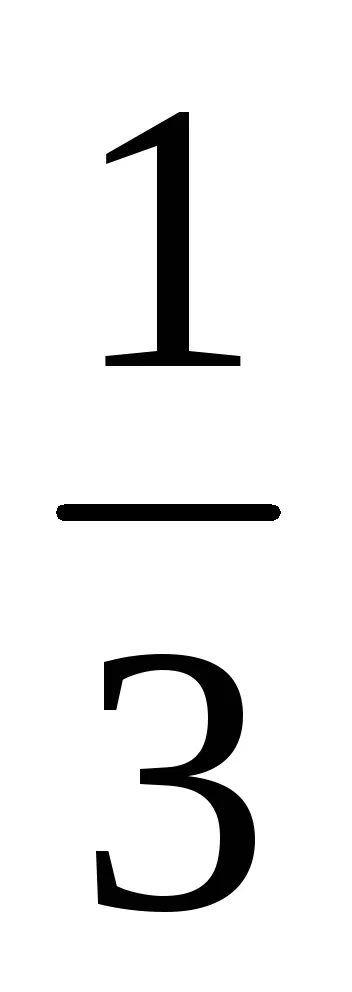
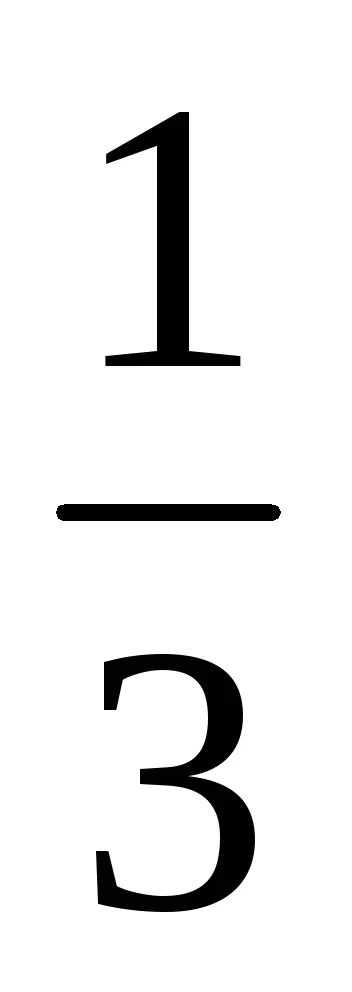
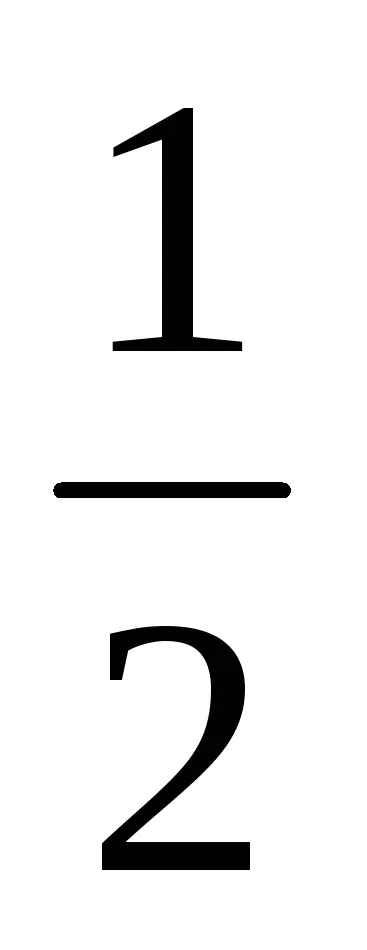
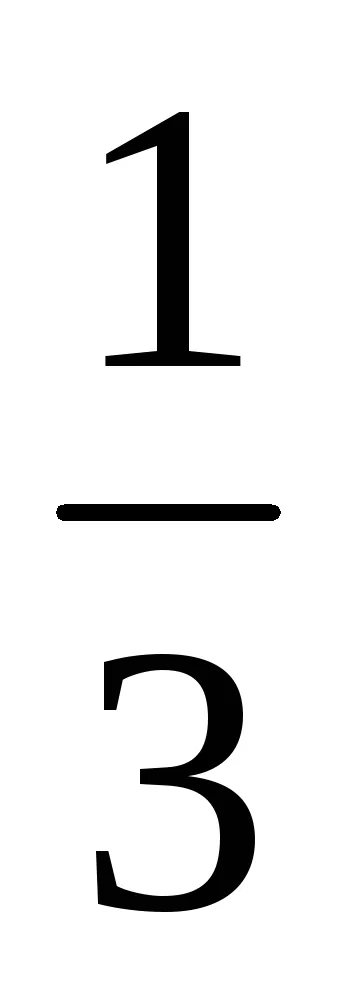
Scutirea de iraționalitate algebrică numitorul fracției
Cursul școlar pentru rezolvarea anumitor tipuri de probleme pentru eliberarea iraționalității în numitorul fracției este suficientă pentru a se multiplica numărătorul și numitorul de numărul de numitor conjugat.
Aici, la numitorul formulei este activat multiplicare Acronim (diferența dintre pătrate), care permite libera a iraționalitate la numitor.
2. A scăpa de iraționalitate în numitorul fracției
t =
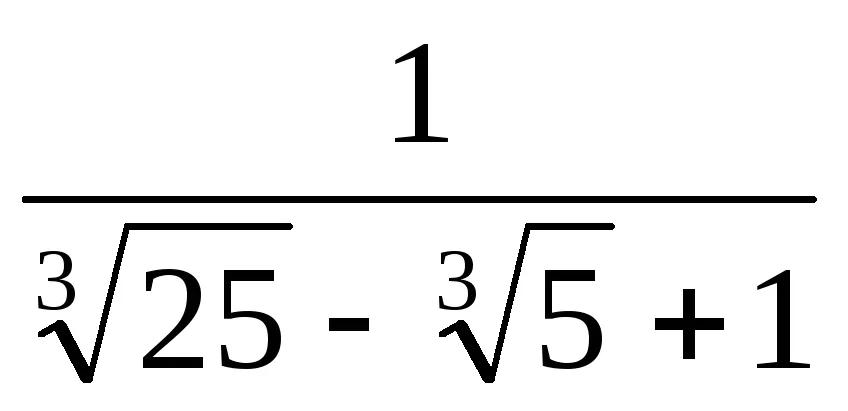
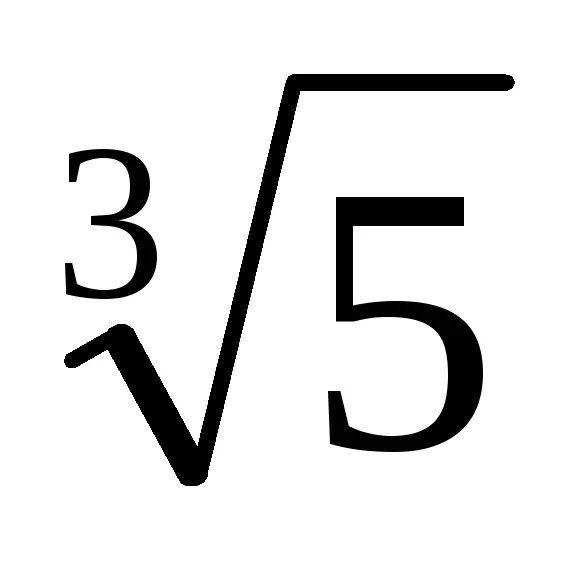
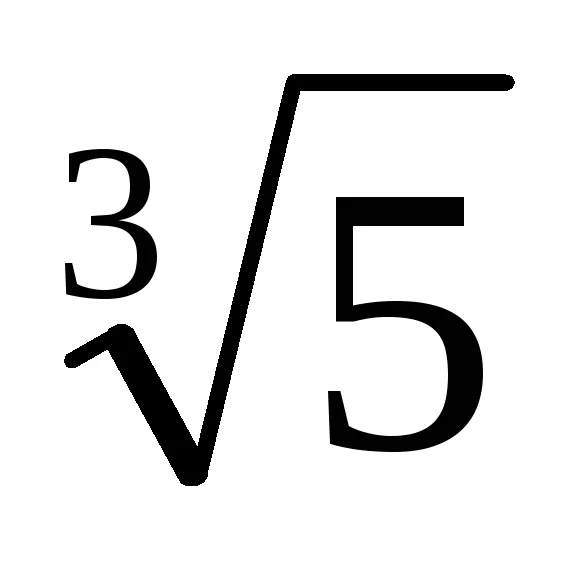
În situațiile în care formulele de multiplicare prescurtate nu funcționează, puteți utiliza alte tehnici. Mai jos formulăm o teorema, dovada care, în special, permite algoritmul pentru a găsi de relief de la iraționalitatea în numitorul fracției în situații mai complexe.
Definiția 6.1. Numărul z se numește algebric peste polemF. dacă există un polinom f (x)
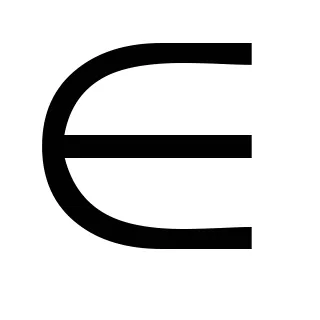
Determinarea 6.2.Stepenyu algebric peste polemFchislaz numit gradul polinomului ireductibilă peste câmpul F p (x)
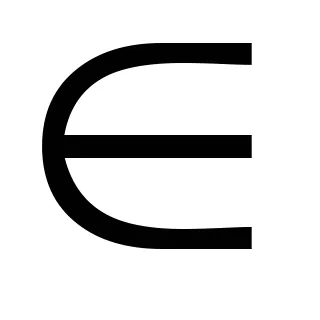
Exemplu. Arătăm că numărul z =
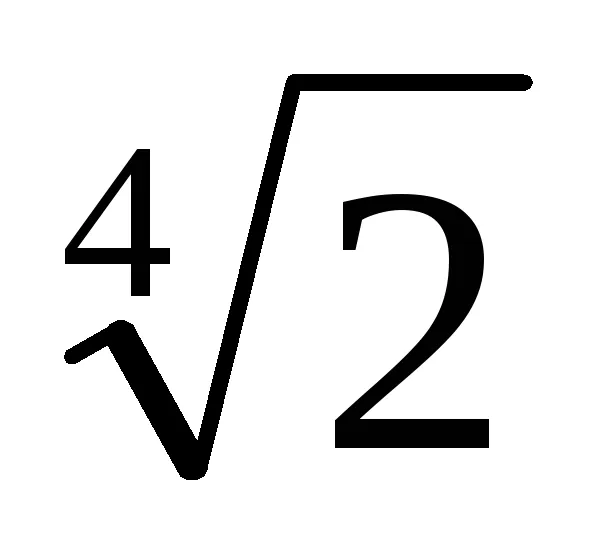
Am găsit un polinom ireductibil deasupra p câmpul Q (x), a cărei rădăcină este x =
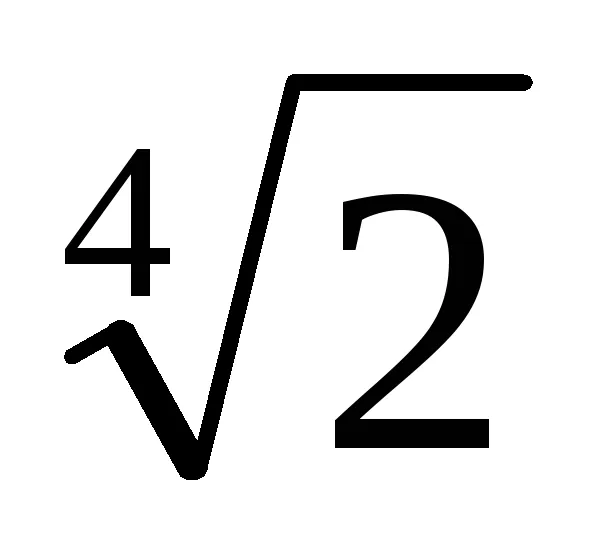
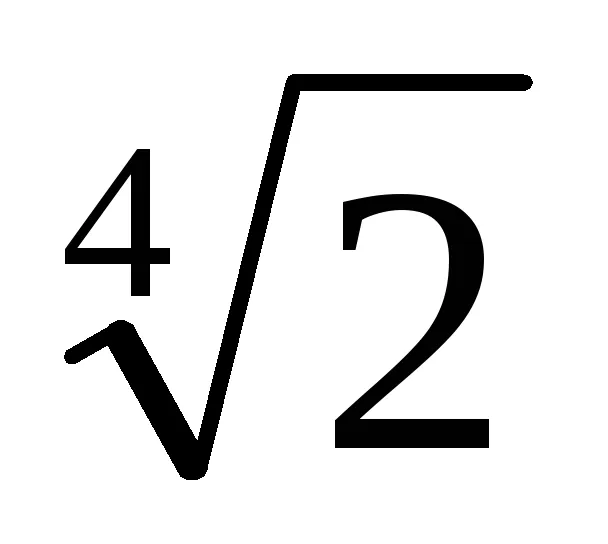
Teorema 6.3 (eliberarea unui iraționalitate algebric la numitor) numarul algebrică .Pustz- peste polemFstepenin. Expresia vidat =
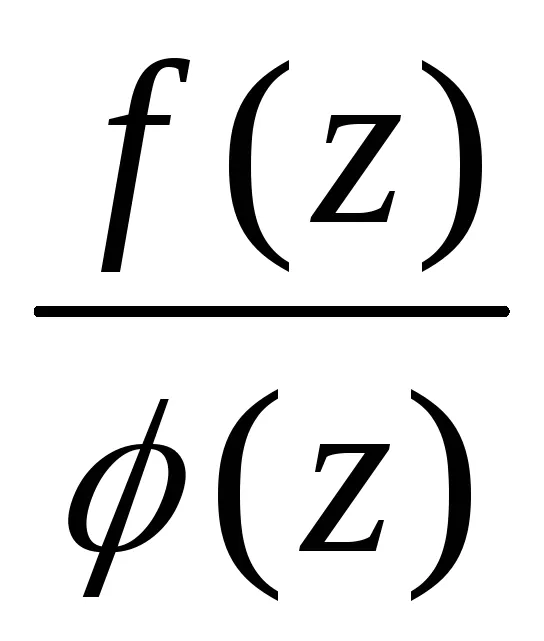

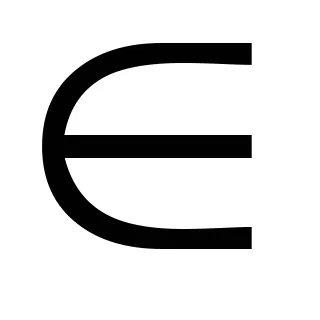

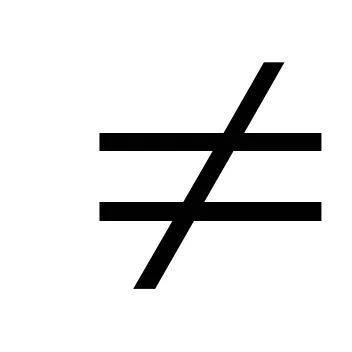
Acesta poate fi reprezentat în mod unic în forma:
t = cn-1zn-1 + cn-2zn-2 + ... + C1z + c0. CI
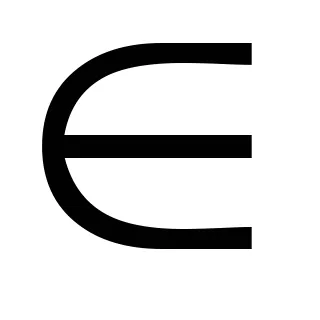
Eliberarea algoritmului iraționalității va demonstra un exemplu specific în numitor.
Exemplu. Gratuit de la iraționalitatea la numitor:
1. numitorul fracției este valoarea polinomului

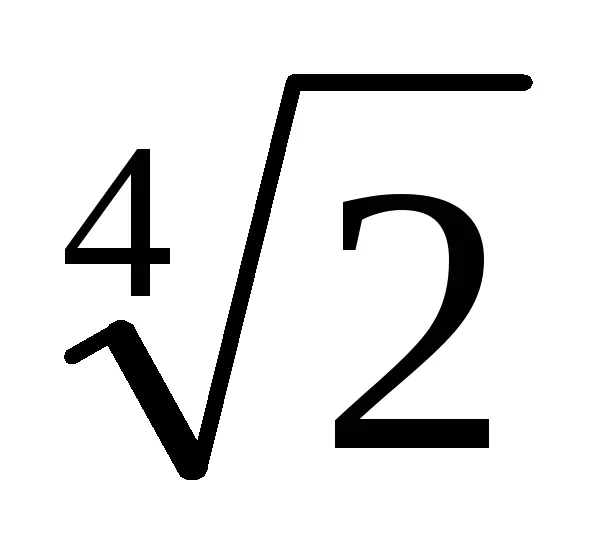
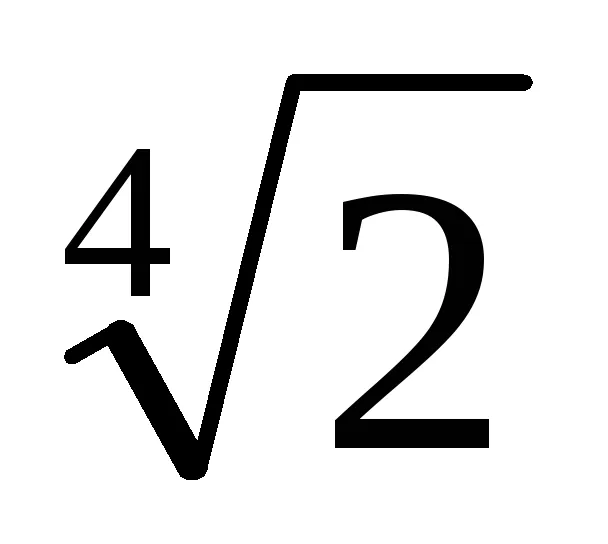
2. Găsiți extinderea liniară a GCD (

-x-2 -
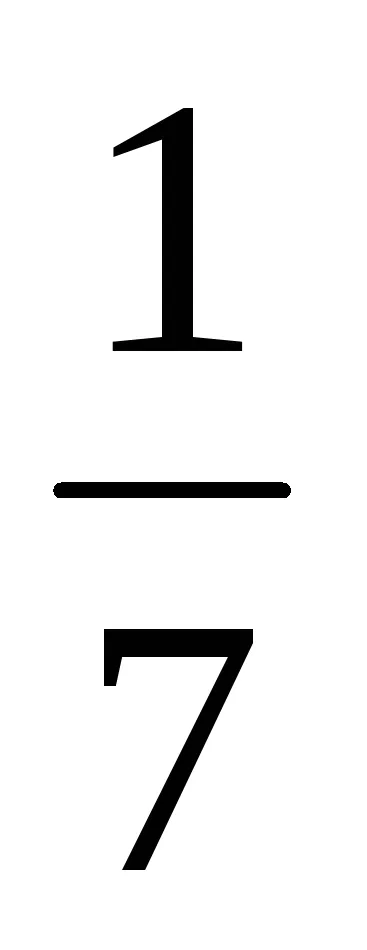
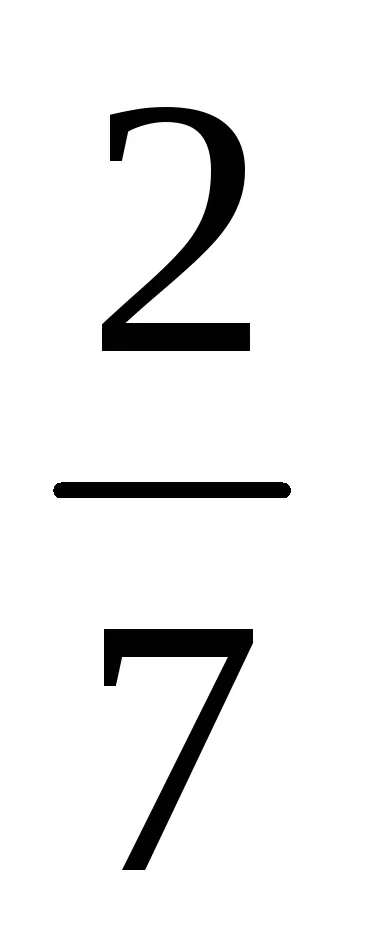
Deci, GCD (

Scriem secventa Euclid, folosind notația de polinoame.
p (x) =




Substituind în ecuația 7 = r2 (x) =




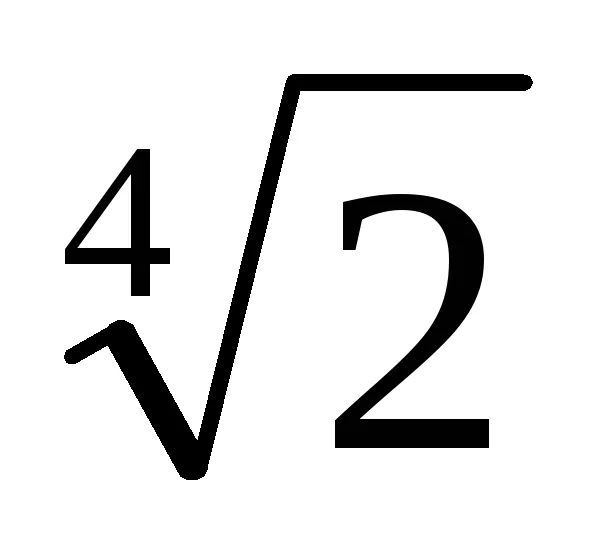
(1 -
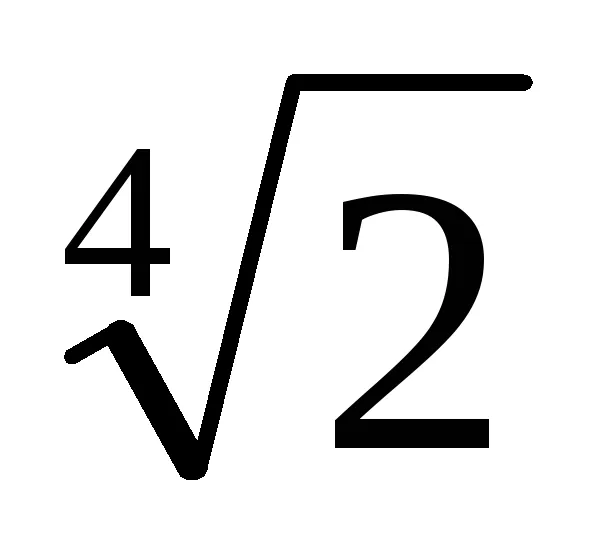
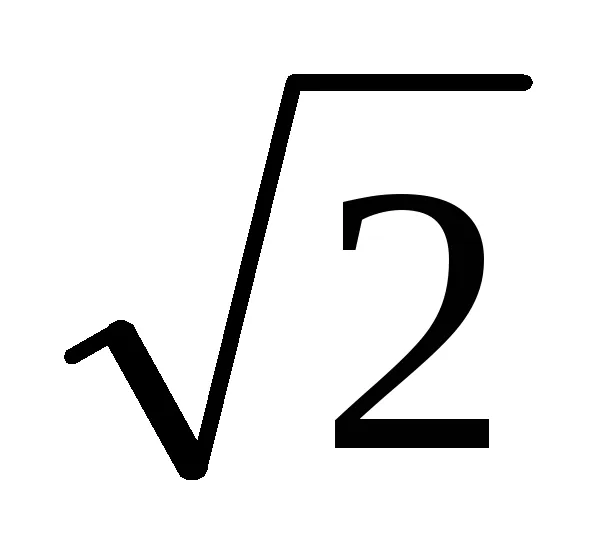
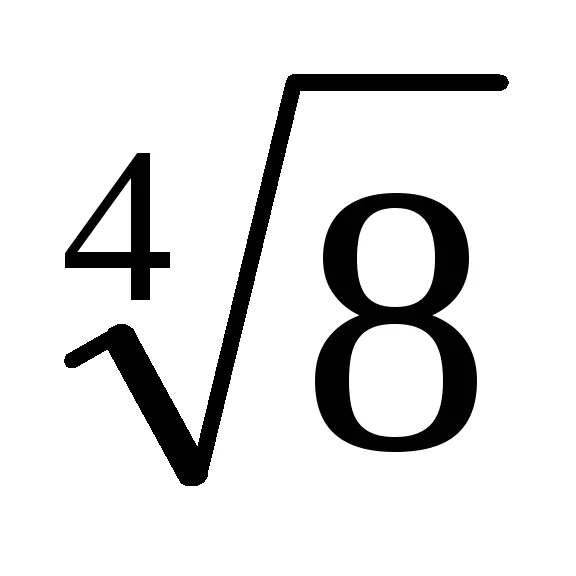
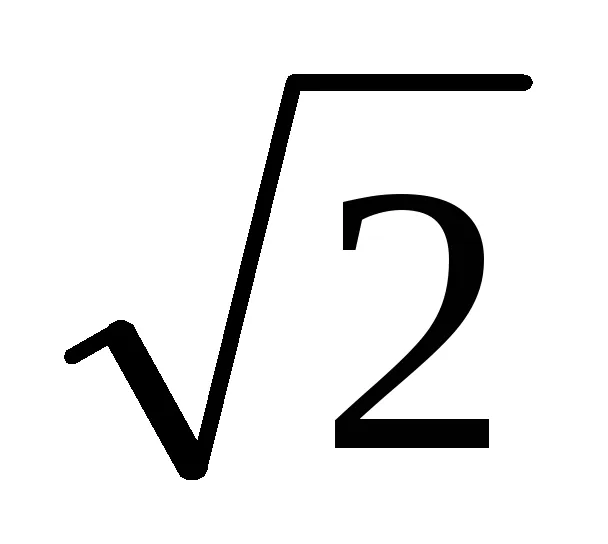
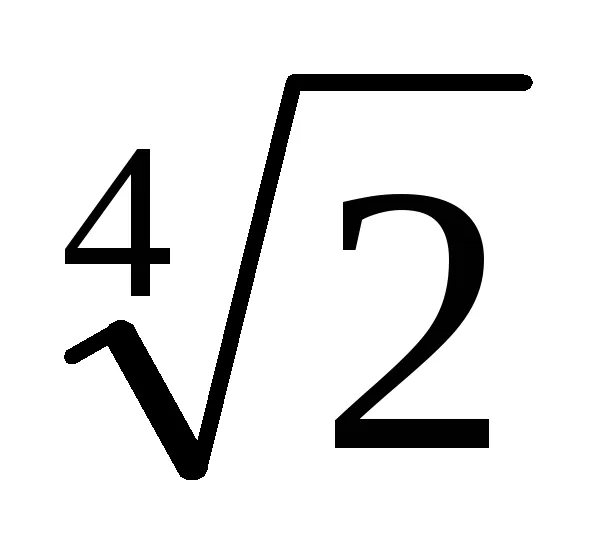
3. Din ecuația (1) implică faptul că dacă numitorul înmulțit cu numărul de t m = [1 + (-
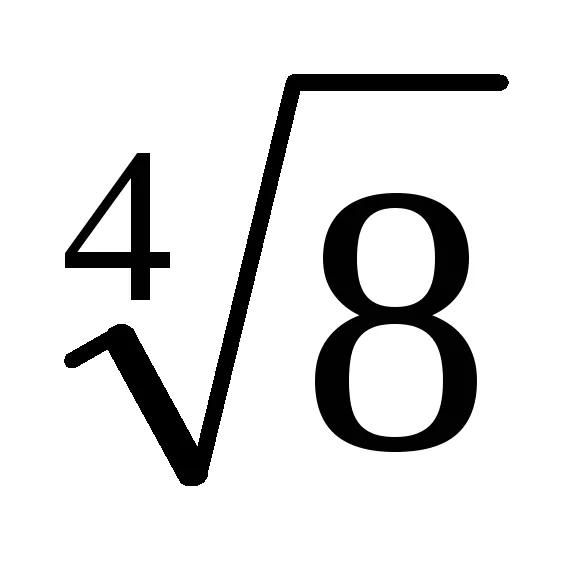
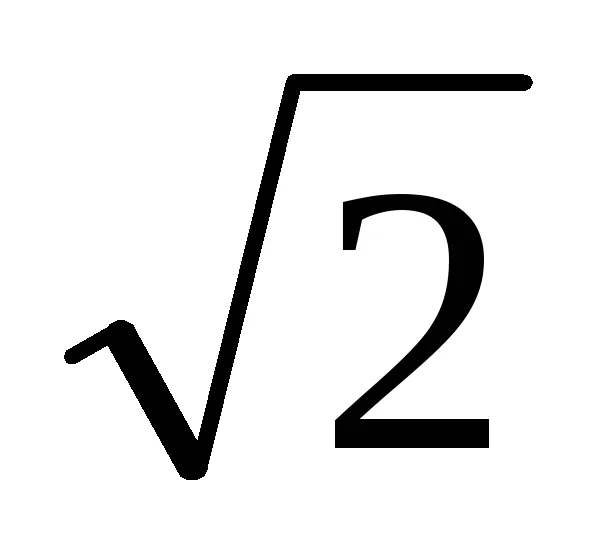
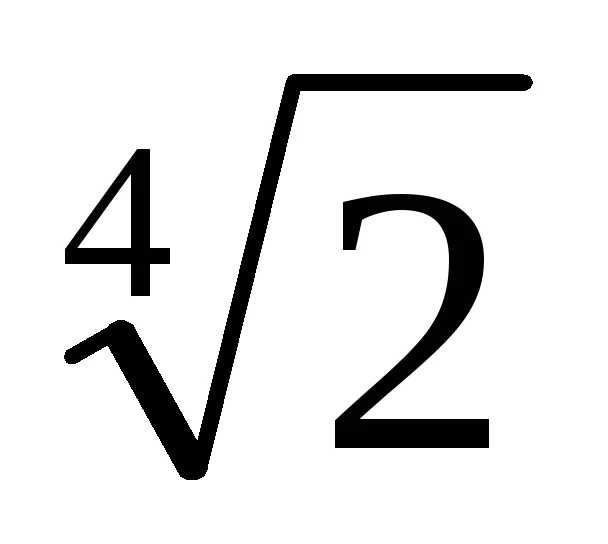
METODOLOGIE 16. Lecția Subiect: Vizualizare standard polinomul
Tipul lecției: o verificare lecție și controlul de cunoștințe și abilități
- verifica abilitățile polinomiali duce la formularul standard
- să dezvolte gândirea logică, atenția elevilor
1. Completați propozițiile:
a) expresie, care cuprinde o sumă de monoamele menționate ... (polinomial).
b) un polinom constând din monoamele standard și care nu conțin astfel de termeni se numește ... (polinomială standard).
c) cel mai înalt grad de monoamele care intră într-un polinom se numește formularul standard ... (gradul de polinomului).
g) Înainte de a determina gradul de necesitate ... (să-l aducă la un formular standard).
d) Pentru a determina valoarea nevoii polinom de a face mai întâi ... (ne imaginăm un polinom în formă standard), a doua ... (valoarea insert a variabilei în expresie).
2. Găsiți valoarea unui polinom:
3. Adu-un polinom la formularul standard de:
4. Adu-un polinom la formularul standard si afla pentru ce valori ale lui x valoarea este de 1: