Punctul apartine segmentului, algoritmi geometrice, programmirovanie-DLA-sshool
Lecția din seria „algoritmi“ geometrice
Bună ziua, dragă cititor!
Astăzi ne uităm la o altă sarcină tipică a unei serii de algoritmi geometrice. Scrieți o funcție care va verifica afilierea orice punct al segmentului. având în vedere coordonatele de început și de sfârșit.
Pentru a pune în aplicare comparații pe date reale a scrie mai multe două funcții: EqPoint () funcție, care va verifica dacă cele două puncte coincid în avion și funcția RealMoreEq (). care va fi utilizat pentru a verifica relația „> =“ (mai mare sau egal cu). Motivul pentru introducerea funcții speciale pe care le cunoaștem deja.
Sarcină. Verificați dacă punctul aparține segmentului.
Lăsați punctele - punctele de început și de sfârșit ale segmentului. - un punct arbitrar în avion.
Un vector pornind de la punctul și punctul de sfârșit vor avea coordonate (x2-x1, y2-y1).
Dacă P (x, y) - un punct arbitrar, coordonatele vectorului sunt egale cu: (x-x1, y - y1).
Punctul P va aparține segmentului în cazul în care:
- Vectori și coliniare (zero produsului vectorial):
. și anume (X-x1) (y2-y1) - (y-y1) (x2-x1) = 0 - Abscisa punctului de P satisface condiția sau. În caz contrar, punctul va fi pe linia spre stânga sau la lungimea corectă.
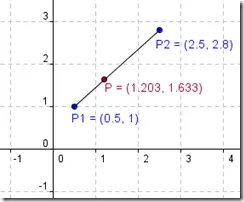
Rezultatele programului.
Introduceți coordonatele punctelor: x1, y1, x2, y2, x, y
1 2.5 2.8 0.5 1.203 1.633
Da.
Rezultatele testelor pentru GeoGebra programului:
AtOtres Astăzi, am scris () funcția. care testează un punct arbitrar care aparține segmentului, având în vedere coordonatele sale.
A introdus două funcții suplimentare: EqPoint () și RealMoreEq (), pentru a pune în aplicare comparații pe date reale. Primele verifică dacă cele două puncte de pe același plan, iar al doilea - este folosit pentru a testa relația „> =“.
În următoarea lecție, pe baza unor proceduri scrise anterior, scrie procedura de determinare coordonatele punctului de intersecție a două segmente.
Cu aceasta vă spun la revedere de la tine. Ne vedem în lecția următoare.
Partajați-le cu prietenii tăi
Vă mulțumim pentru formula!
Bună ziua. Mulțumesc. un mare ajutor pentru lecția, dar există o singură întrebare. Ați indicat că coliniaritate vectorilor trebuie sa satisfaca ecuatia (x-x1) (y2-y1) - (y-y1) (x2-x1) = 0 este produs vectorial yavlyaetsya. Nu înțeleg acest punct. Produsul vector este un vector. O ecuație de căutare de mai sus, după cum am înțeles ecuație derivată dintr-o trecere dreaptă prin două puncte de pe plan (x-x1) / (x2-x1) = (y-y1) / (y2-y1). Corectați-mă vă rog, dacă mă înșel, dar mi se pare că eroarea de aici.
- unghiul dintre vectorii, P1P2 și P1P = 0, aceeași pentru P2P1 și P2P. Ca alternativă, pentru viteza, produsul intern al acestor vectori> = 0, deoarece valorile reale ale unghiurilor nu avem nevoie.
Site-ul este creat pentru studenți și profesori de informatică. Pe site-ul puteți găsi lecții în limbaje de programare Pascal, Lazarus, și Basic.Net vizuală.
În plus, aici veți găsi lecții în 3-D program de modelare Blender.