Proprietățile determinanților matrici
Să ne formulăm proprietățile de bază ale factorilor de determinanți inerente ale tuturor ordinelor. Unele dintre aceste proprietăți pentru a explica factorii determinanți ai al treilea ordin.
1. Dacă (coloană) matrice rând constă din zerouri, atunci determinantul său este 0.
2. În cazul în care toate elementele din orice rând (coloană) a matricei este înmulțită cu un număr. atunci determinantul său este înmulțită cu acest număr.
Dovada. Să determinantul matricei originale este. Pentru a determina primul rând al matricei se multiplica pe. Obținem un nou factor determinant. care se extinde pe elementele din primul rând:
Pentru determinantul factor comun poate face orice linie sau coloană, în contrast cu matricea ca un semn care poate fi luată numai factor comun al tuturor elementelor.
3. Atunci când se deplasează cele două rânduri (coloane) ale determinantul modificărilor matricei la semnul opus.
4. Dacă matricea conține două rânduri identice (coloana), atunci determinantul este zero.
Dovada. Într-adevăr, rearanja rândurile (coloane). Pe de o parte, determinantul nu se schimba, dar, pe de altă parte, de proprietate de 3 modificări semn, adică . în cazul în care.
5. În cazul în care elementele celor două rânduri (coloane) ale matricei sunt proporționale, determinantul său este zero.
Dovada. Să presupunem pentru definiteness care sunt proporționale cu prima și a doua rânduri. Apoi, luând un factor de proporționalitate. Obținem pe proprietate 2 :. care are două rânduri identice și de proprietate 4 este 0.
6. Determinantul nu se modifică în cazul în care acesta este de a înlocui coloanele șir, și vice-versa.
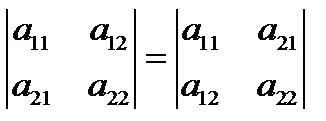
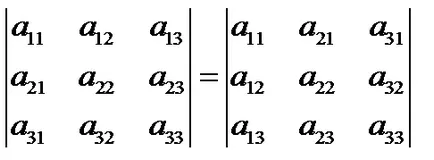
Pentru a dovedi suficientă pentru a calcula valoarea determinantului, stând în picioare în ecuațiile de pe stânga și dreapta.
7. Dacă fiecare element coloană (rând) a determinantului este suma celor doi termeni, factorul determinant poate fi reprezentat ca o sumă a doi factori determinanți, dintre care unul este în coloana (rând) este primul dintre termenii menționați, iar celălalt - al doilea; elemente de la alte locuri, toate cele trei factori determinanți ai acestora:
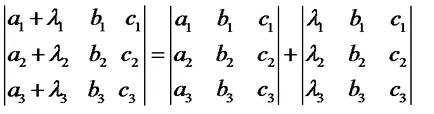
8. Determinantul matricei nu se schimbă dacă elementele unei matrici rând (coloană) pentru a adăuga elemente alt rând (coloană), înmulțit anterior cu același număr.
9. Determinantul produsului a două matrice pătrate este produsul determinanților lor :. în cazul în care. și - matricea ordine.