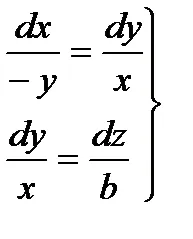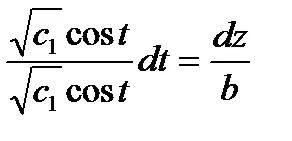proprietăți de gradient - studopediya
1 0 Gradientul este direcționat de-a lungul normala la nivelul suprafeței (sau la o linie de nivel atunci când un câmp este plat).
2 0 Gradientul este îndreptat în direcția creșterii funcției câmpului.
3 0 modulul gradientului este câmpurile punctului napravleniyuvdannoy cele mai derivate:
Aceste proprietăți se un gradient caracteristic invariant face. Ei spun că vectorul grádu indică direcția și magnitudinea cele mai mari schimbări în domeniul scalară la un anumit punct.
Observația 2.1. Dacă funcția U (x, y) este o funcție de două variabile, vectorul
Acesta se află în planul oxi.
Fie U = U (x, y, z) și V = V (x, y, z) derivabila M0 (x, y, z) funcția punctului. Apoi, avem următoarele egalități:
a) grad () =; b) grad (UV) = VgradU + UgradV;
a) grad (U V) = GRADU gradV; g) g) grad =. V;
d) GRADU (= GRADU, în care. U = U () are un derivat.
Exemplul 2.1. Funcția Dată U = x 2 + y 2 + z 2. Se determină gradientul funcției în punctul M (-2, 3, 4).
Decizie. Conform ecuației (2.2)
,
.
Suprafețele de nivel ale câmpului scalar sunt o familie de sfere x 2 + y 2 + z 2. GRADU vector = (- 4, 6, 8) este un vector de avioane normale.
Exemplul 2.2. Găsiți gradientul unui câmp scalar U = x-2y + 3Z.
Decizie. Conform ecuației (2.2)
Suprafețele de nivel ale câmpului scalar sunt plane
x-2y + 3z = C; GRADU vector = (1, -2 și 3) există un vector normal al familiei de avioane.
Exemplul 2.3. Găsiți maxim de ridicare panta suprafeței U = x y la punctul M (2; 2; 4).
Exemplul 2.4. Găsiți versorul normal la nivelul suprafeței câmpului scalar U = x 2 + y 2 + z 2.
Decizie. suprafață plană de interior sfera Fields x 2 + y 2 + z 2 = C (C> 0).
Gradientul este normal la suprafața de nivel, astfel încât
. Definește un vector normal la suprafața stratului de la un punct M (x, y, z). Pentru a obține unitatea de vector de expresie normală
.
Exemplul 2.5. Găsiți gradientul U =. unde vectorii constant, r este vectorul raza unui punct.
apoi:
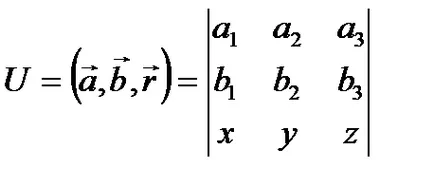
Exemplul 2.6. Găsiți gradientul distanței. unde P (x, y, z) - Punct câmp studiat, P0 (x0, y0, z0) - un punct fix.
Decizie. Avem - o direcție vector unitate.
Exemplul 2.7. Găsiți unghiul dintre gradientul funcției în punctul M0 (1,1).
Decizie. Găsim înclinări acestor funcții în punctul M0 (1.1), avem
; Unghiul dintre GRADU și gradV un punct M0 se determină din ecuația
Exemplul 2.8. Găsiți derivatul în direcția vectorului rază este
Decizie. Găsim gradientul acestei funcții:
Substituind (2.5) (2.4) în randamente
Exemplul 2.9. Găsiți punctul M0 (1, 1, 1), direcția de cea mai mare schimbare a unui câmp scalar U = xy + yz + xz și magnitudinea celor mai mari schimbări în acest moment.
Decizie. Cele mai mari schimbări în direcția indicată de câmp vectorial grad U (M). L-am găsit:
Și apoi. Acest vector determină direcția cea mai mare creștere a câmpului în punctul M0 (1; 1; 1). Amploarea cea mai mare variație a câmpului de la acest punct este egal cu
.
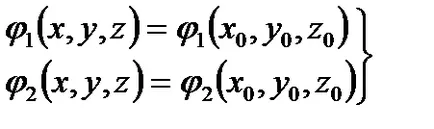
Exemplul 3.1. Găsiți liniile vectoriale ale unui câmp vectorial care este un vector constant.
Decizie. Au asa
Ecuații diferențiale de linii vectoriale
Înmulțirea numărătorului și numitorul fracției pentru prima x, iar a doua y-on, pe ultimul pachet și adăugați termwise z. Folosind proporțiile proprietății, obținem
. deci XDX + ydy + ZDZ = 0, ceea ce înseamnă
x 2 + y 2 + z 2 = A1. A1 -const> 0. Acum înmulțim numărătorul și numitorul primei fracțiuni (3.3) pe c1. doua c2 -on. a treia c3 și adăugarea, termenul de termen, obținem
. unde c1 dx + c2 dy + c3 dz = 0
Ecuațiile necesare de linii vectoriale

Aceste ecuații arată că liniile vectoriale sunt rezultatul intersecției sfere având un centru comun la origine, cu un plan perpendicular pe vectorul. Acest lucru implică faptul că liniile vectoriale sunt cercuri ale căror centre sunt pe o linie dreaptă care trece prin origine, cu direcția vectorului. Cercuri plan perpendicular pe respectiva linie dreaptă.
Exemplul 3.2. Găsiți o linie de câmp vectorial care trece prin punctul (1,0,0).
Decizie. Ecuații diferențiale de linii vectoriale
prin urmare, avem