Probleme interesante cu conținut practic
1. Teoria Repetiție
a) Similaritatea triunghiuri.
b) segmente proportionale din cerc.
2. cuvintele Maestrului despre scopul acestui tutorial
Geometrie - nu este doar știința proprietăților triunghiuri, paralelograme, cercuri. Geometrie - este o lume întreagă, care ne înconjoară de la naștere. După tot ceea ce vedem în jurul nostru, într-un fel sau altul legate de geometrie, nimic nu scapă privirea atent. Geometria ajută o persoană să se plimbe prin lume cu ochii larg deschiși, să învețe uite cu atenție în jurul valorii și a vedea frumusețea lucrurilor obișnuite, ceas și cred că, cred că și trage concluzii.
La lecția vom discuta sarcini interesante pentru a rezolva, care va ajuta la cunoașterea geometriei, că elevii au în clasa a opta.
3. Prezentarea unuia dintre elevii cu un scurt mesaj despre Conan Doyle


Dar el este foarte bun, probabil știa geometrie. În poveste „Ritualul Musgrave“, a descris ca Sherlock Holmes a trebuit să determine în cazul în care la sfârșitul anului va fi umbra copacului ulm, care a fost tăiat în jos. El cunoștea înălțimea copacului mai devreme. Sherlock Holmes a explicat acțiunile sale:“... am conectat cu două tije, care mi-a dat șase picioare, iar eu și clientul meu sa dus la locul unde a crescut odată ulm. Am blocat un pol în pământ, a declarat direcția umbrei și a măsurat-o. A fost de nouă picioare înălțime.
Mai mult calculele mele au fost într-adevăr destul de ușor. În cazul în care stick-ul este de șase picioare înălțime aruncă o umbră de nouă picioare, înălțimea arborelui de șaizeci și patru picioare aruncat o umbră în nouăzeci și șase picioare, și direcția de una sau alta, desigur, va fi la fel. "
Problema 1. măsurarea înălțimii arborelui
Pentru a măsura înălțimea arborelui BD a fost preparat triunghi AB1 C1 în unghi, cu un unghi A = aproximativ 45 și ținându-l pe verticală, este deplasat pe distanța la care, pornind de-a lungul AB1 ipotenuza. a văzut în vârful unui copac Q. Care este înălțimea de copac, în cazul în care distanța
AC = 5,6m și înălțimea de 1,7 m înălțime persoanei?
1) Deoarece A este comună ambelor triunghiuri și AC1 B1 și DIA (prin ipoteză) directă (de exemplu, egal în 90), CA1 B1 și DIA - ca (pe baza similarității dintre cele 2 colțuri).
2) Apoi AB1 C1 = ABC = 45 o. => BC = AC = 5,6m, dar pentru a obține lungimea, trebuie să adăugăm, de asemenea, înălțimea, și anume lungimea arborelui DB = 7,3m.
Problema 2. Turnul inamic
segment de drum deschis stocat pe o bandă de lățime de 50 m AB; un post de observare inamic este situat în partea superioară a înălțimii turnului clopot MN = 22M. Ce înălțime ar trebui să facă masca HF pe verticală la o distanță de 500 m de la turnul de clopot pentru a închide drumul de la observatorul inamic?
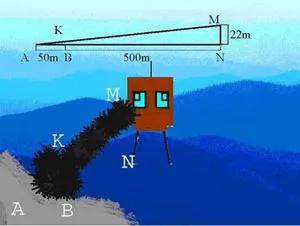
AMN, AB = 50m,
MN = 22m,
BN = 500m
AMN (2 colturi Nd: A - general, AVK și AMN - drept, iar în cazul în care triunghiuri sunt similare, atunci toate elementele sale, de asemenea, sunt ca cuvinte, și, prin urmare, m ...
Obiectivul 3. Teren dintr-o privire, atunci când sunt în cer într-un balon
Cât de departe poate fi văzut dintr-un balon care a crescut la înălțimea de 4 km deasupra Pământului (aproximativ egală cu raza de 6370 km Pământului)?
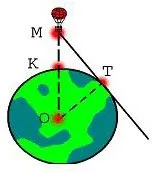
1. Prin teorema tangenta la cercul perpendicular pe tangenta raza realizată la punctul de contact, adică 90 = OTM.
2. MO = 4 + 6370 = 6374 km,
3. Apoi, teorema lui Pitagora:
MT 2 2 + OT = MO 2
MT 2 = 2 MO - OT 2
MT = 112,9 km
Sarcina 4. Determinarea distanței de la navele de pe mare
Adresa probleme practice specifice vechi pot găsi aplicații în prezent, și, prin urmare, merită o atenție.
Istoria geometriei păstrează o mulțime de tehnici de rezolvare a problemelor pentru a găsi distanța. Determinarea distanței față de navele de pe mare, - una dintre acele sarcini care trebuie rezolvate în două moduri.
Găsiți distanța de la punctul A situat pe malul la navă
Prima cale. Lăsați nava se află la punctul K, iar observatorul de la punctul A este necesară pentru a determina distanța navei spațiale. Prin construirea unui drept punct de unghi A, este necesar să se amâne pe mal două segmente egale AB = BC. La punctul C din nou construi un unghi drept, observatorul trebuie să urmeze perpendiculara în sus până când ajunge la punctul D, din care vehiculul K și punctul B ar fi vazut sa se intinda pe o linie dreaptă. VSD triunghiuri dreptunghiulare și bak sunt, prin urmare, CD = AK și CD întindere pot fi măsurate direct.
A doua metodă. numita metoda triangulație. Am găsit aplicații în astronomie. Cu ajutorul distanțelor măsurate la corpurile cerești. Această metodă constă în 3 etape:- Măsurarea unghiurilor 1 și 2, iar distanța AB.
- A'V'K Construcție „cu unghiuri 1 și 2 la nodurile A“ și B „, respectiv.
- Având în vedere similitudinea triunghiuri ABK, A'V'K „și egalitatea, lungimea cunoscută a segmentului AB, * o“ „și“ B „nu este dificil de a găsi o lungime de segment AK.


Și această problemă este rezolvată pe baza teoremei: Dacă două acorduri se intersectează într-un cerc, atunci produsul lungimilor porțiuni de una dintre ele este egală cu produsul dintre lungimile celorlalte părți.
Uită-te la imagine, și odată ce devine clar, ca adâncimea lacului este (x):
Raspuns: 17.05 inch.
La lecția pe care au fost discutate cele mai presante probleme legate de măsurătorile geometrice pe teren - definirea înălțimii obiectului, găsind distanța până la obiecte inaccesibile. Aceste obiective sunt de interes practic considerabil, să consolideze cunoștințele dobândite în geometria și pot fi utilizate pentru lucrări practice. Valoros este faptul că soluțiile lor nu au nevoie de cunoștințe mai mult decât în valoare de 8 clase.
Elbrus (Caucaz) se ridică deasupra nivelului mării până la 5600m. Cât de departe poate fi văzut de pe vârful acestui munte?
M - o supraveghere post înălțime h metri deasupra pământului; Pământ raza R, MT = d este cea mai mare distanță vizibilă. Demonstrați că.
Găsiți distanta de insula, situat pe malul lacului, la punctul B de pe coasta. (Pe insula să preia punct).
Partea de sus a muntelui poate fi văzut de la punctul A la un unghi de 38 # 01; 42“, iar abordarea pe munte la vârf de 200m a fost vizibil la un unghi de 42 # 01;. Găsiți înălțimea muntelui.
1. Sergeev ÎN Olekhnik SN Gashkov SB "Aplicare matematica", Wiley Stiinta 1989.
2. MB vrac Balk GD „Matematica după școală,“ M. Educație 1971.
3. Chetverukhin NF "Metode de construcții geometrice", M. Uchpedgiz 1952.
4. Kosyakin AS Nikulin AS Smirnov "Gestionarea terenurilor", M. Nedra 1988.
6. AV Tkachev Acasă Matematica Grad 8
8. Dacă Sharygin Erganzhieva LN Geometrie vizuală.