Operații pe matrici - studopediya

operațiune Proprietăți plus matrice

Pentru orice matrici A, B și C sunt aceeași dimensiune egalitățile:

1. A + B = B + A (comutativitatea);

2. (A + B) + C = A + (B + C) = A + B + C (asociativitatea).

Produsul a matricei A = (aij) numărul L este matricea B = (bij) de aceeași mărime ca și matricea A. în care bij = l aij. „I, J.

Proprietățile înmulțirii matricei în numărul

2. l (A + B) = LA + LiN (distributiv peste matrice plus).

3. (l + m) A = LA + mA (distributivă față de numerele de adiție).

Produsul AB A si B (dimensiuni m'n și n'.R respectiv) este dimensiunea matricei C m'r. astfel încât Sij = ai1b1j + a12b2j + ... + aik bkj + ... + ain bnj =

.

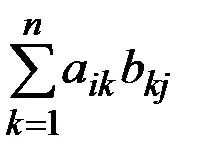
Astfel, fiecare element Sij. situat în ith rând și j th coloană a matricei C este suma produselor elementelor corespunzătoare ale rândului i -lea al matricei A și j coloana -lea a V. matrice

Element Prepararea Sij este reprezentat schematic așa

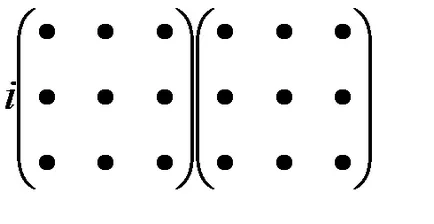
AB Produs există numai în cazul în care numărul de coloane ale matricei A este egal cu numărul de rânduri ale matricei.

Proprietățile operației de înmulțire matrice

1. (AB) C = A (BC) = ABC (asociativitatea).

2. (A + B) C + BC = AC (distributivitatea).

3. A (B + C) = AB + AC (distributivitatii).

4. AV¹VA (off-line comutativitatea).

Switching (sau permutare) sunt matrici A și B, pentru care AB = BA.

Matricea obținută din aceasta înlocuind fiecare dintre liniile sale cu același număr de coloană, numită matrice, transpusa a (A notat T).

1.3.1. Găsiți combinații liniare ale matricelor prestabilite:

1.3.2. Găsiți produsul matricelor AB și BA (dacă există):

a)

; b) A = (4 0 -2 3 1), ;

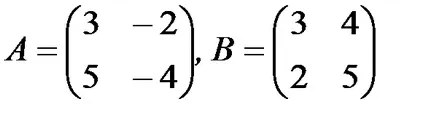
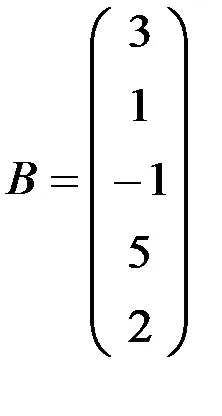
1.3.3. Verificați dacă matricele fac naveta:

1.3.4. Găsiți produsul matricea A și AA T T A:

a)

b) A = (1 2 3 4); c) .

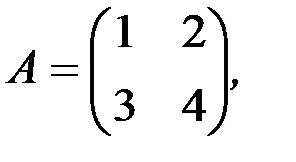
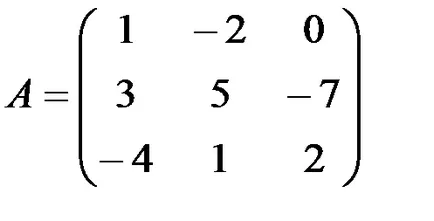
1.3.5. Pentru a găsi combinații liniare de matrici:

1.3.6. Găsiți lucrări de AB și BA (dacă este posibil):

1.3.7. Găsiți lucrări de AA T și A T A: