O matrice pătrată
A patra comandă matrice pătrată. Elementele principale formează matricea A II pătrat diagonală. De exemplu, diagonala principală a matricei 4x4 din figură conține elemente a11 = 9, a22 = 11, a33 = 4, A44 = 10.
În matematică, o matrice pătrată - o matrice. în care numărul de rânduri egal cu numărul de coloane, iar acest număr se numește ordinea matricei. Orice două matrici pătrate de aceeași ordine pot fi adăugate și multiplicate.
matrici pătrate sunt adesea folosite pentru a reprezenta mapări liniare simple - cum ar fi tulpina [en] sau rotație. De exemplu, dacă R - o matrice pătrată reprezentând rotație (matricea de rotație) și v - vector coloană. determinarea poziției unui punct în spațiu, produsul Rv oferă un alt vector, care determină poziția punctului după rotație. Dacă v - vector rând. aceeași conversie poate fi obținută folosind unde T. R T VR - matricea R transpusa.
matrici diagonale și triunghiulare
În cazul în care toate elementele din afara diagonalei principale sunt zero, A este o diagonală. Dacă toate elementele de mai sus (mai jos) diagonalei principale sunt zero, A este numit inferior (superior) matricea triunghiulară. matrice triunghiulara ale cărei elemente diagonale sunt egale cu 1, denumit unitriangular [2] [3].
matricea identitate
Matricea de identitate En dimensiune n - este n × n matrice în care toate elementele de pe diagonala principală sunt egale cu 1 și celelalte elemente sunt egale cu 0 (adesea folosit în locul literei litera E I [4]) [1]. Astfel,
multiplicarea matricea identității de matrice frunze neschimbat:
Simetric și matricea antisimetrică
O matrice pătrată A. coincide cu transpusa acesteia. adică A = A T. numită simetrică. Dacă A este diferit de semnul unei matrice transpuse, adică A = -A T. atunci A se numește antisimetrică (sau antisimetrică) [4] [5]. În cazul unor matrici complexe ale conceptului de simetrie este adesea înlocuită cu noțiunea de autoadjunct. o matrice care satisface ecuația A * = A. numita Hermitian (sau selfadjoint); Aici asterisc reprezintă o operațiune de conjugare Hermitian. în care semnificația - înlocuirea fiecărui element din matricea transpusa inițial complex conjugat urmat număr de matricea rezultată [6] [7].
Conform teoremei spectrale pentru matrici simetrice reale si matrici hermitian complexe are o bază formată din vectori proprii; în acest fel, orice spațiu vectorial poate fi reprezentat ca o combinație liniară a vectorilor proprii. În ambele cazuri, toate valorile proprii sunt reale. [8] Această teoremă poate fi extinsă la cazul infinit atunci când matricelor au un număr infinit de rânduri și coloane.
Inversarea matricelor
O matrice pătrată A se numește inversabilă sau nesingular. dacă există o matrice B. astfel încât
Dacă există matricea B, este unic și se numește inversul A și înregistrate ca A -1.
matrice certă
Punctele care satisfac ecuația Q (x, y) = 1
(Elipsă).
Punctele care satisfac ecuația Q (x, y) = 1
(Hiperbolă).
Simetric n × n matrice se numește bine definit (respectiv negativ nedeterminată sau definit), în cazul în care pentru toți vectorii nenuli x ∈ Rn corespunzătoare formă pătratică pozitiv
Este nevoie doar valori pozitive (respectiv, valori negative, sau ambele, și altele). Dacă forma pătratică durează numai non-negativ (sau numai non-pozitiv) valoare, o matrice simetrică este numită semidefinite pozitiv (respectiv negativ semidefinite). Matricea va fi incert dacă acesta nu este nici semidefinite pozitiv, nici negativ. [11]
matrice simetrica este pozitiv definită dacă și numai dacă toate valorile proprii sale sunt pozitive [12]. Tabelul din dreapta prezintă două posibile cazuri pentru 2 × 2 matrici.
Dacă utilizați doi vectori diferiți, vom obține o formă biliniară. asociate cu A:
matrice ortogonale
Orthogonal matrice - o matrice pătrată cu elemente reale, ale căror rânduri și coloane sunt vectori ortogonali unități (adică ortonormate). Se poate defini, de asemenea, o matrice ortogonala ca matrice inversă este egal cu transpusa [7]:
O matrice A ortogonale este întotdeauna inversabilă (-1 = A T A), este unitar (A -1 = A *), și normal (A * A = AA *). Determinantul oricărei matrice ortogonale este egală fie +1 sau -1 [14]. Multiplicarea cu o matrice ortogonala definește o transformare liniară aritmetică spațiu R n ^>. care, în cazul unei matrice cu determinant +1 este un viraj simplu. iar în cazul unei matrice cu determinant -1 este o reflecție simplă. sau superpoziție de reflecții și rotație.
Ca urmare a unei matrice A pătrat (tr (A)) este suma elementelor diagonala principală. In timp ce multiplicarea matricelor, în general vorbind, nu comutativ, urme de produs a două matrici este independentă de ordinea factorilor:
Acest lucru rezultă direct din definiția produsului matrice:
De asemenea, trebuie transpusă matrice este egal cu piesa la ea, adică,
determinant
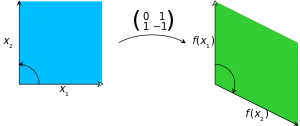
Maparea liniara pe anumite R 2. matricea redusă. Determinantul matricei este -1, și, deși zona paralelogram verde a rămas 1 afișează o schimbare de orientare. Deoarece vectorul sunt sensul acelor de ceasornic, iar imaginile lor sunt în ordine inversă.
DET factor determinant (A) sau | A | matrice pătratică A - este un număr care definește unele proprietăți ale matricei. Matricea este reversibil dacă și numai dacă. atunci când determinantul său este non-zero. Valoarea absolută a determinantului este egală cu suprafața (R2) sau volumul (în R3) a pătratului unității de imagine (sau cub), în timp ce semnul determinantului se potrivește cu orientarea afișajului respectiv - determinantul este pozitiv dacă și numai dacă orientarea este menținută.
Determinant matrice 2 x 2 se calculează cu formula:
Determinant matrice 3 x 3 folosește 6 piese (regula lui sarrus). Mai formula Leibniz [en] generalizează aceste două formule pentru toate dimensiunile [15].
Determinantul unui produs de matrici este produsul factorilor determinanți:
Adăugarea orice rând cu coeficientul pentru o altă linie sau cu orice coloană la un alt coeficient coloană nu alterează determinant. Swapping două rânduri sau coloane determinante conduce la o schimbare în semnul [17]. Folosind aceste operații, orice matrice poate fi redusă la inferior (sau superior) matrice triunghiulară și pentru astfel de matrici determinant este egal cu produsul dintre principalele elemente diagonale, care oferă o metodă de calcul determinantul oricărei matrice. În cele din urmă, Laplace teorema exprimă determinant în ceea ce privește minorii. adică determinanților matrici mai mici [18]. Această teoremă permite determinanții de calcul recursive (începând cu determinantul matricei 1 x 1, sau chiar cu o matrice de factor determinant 0 x 0, care este egală cu 1), care pot fi considerate ca formula Leibnitz echivalentă. Detectoarele pot fi utilizate pentru rezolvarea sistemelor liniare folosind metoda lui Cramer [19].
Vectori și valori proprii
Numărul X și un vector v nenul. satisface ecuația
numit eigenvalue și eigenvector de A, respectiv [20]. Numărul este o valoare proprie λ n x n matricea A dacă și numai dacă un -λE nu invers, echivalentul
Din pA polinomul necunoscut [en] X. a primit det determinant (XE -A), numit polinomul caracteristic al matricei A. Acest polinom normalizat [en] * gradul n. Astfel, ecuația (λ) pA = 0 are maxim n soluții diferite, adică valori proprii [21]. Aceste valori pot fi complexe, chiar dacă toate elementele matricei A sunt reale. Conform teoremei lui Hamilton - Cayley. pA (A) = 0. adică prin substituirea matricei în sine în polinomul caracteristic obține matricea zero, [22].