Momentul de inerție, student la fizica, elev, articole și discuții privind educația

Atunci când o rotație a corpului solid în jurul unei axe fixe de puncte ale corpului individuale descrie un cerc, al cărui centre se află pe axa de rotație. Fundamentele cinematicii ale mișcării de rotație sunt stabilite în secțiunea 1.5.

Pentru a descrie mișcarea de rotație a unui solid, se introduce conceptul de moment de inerție.

Momentul de inerție I a punctului material se numește mărime fizică scalară determinată de produsul din masa cerc mna pătrat de rază R, prin care se poate deplasa în raport cu unele arbitrar ales axa OO „(Fig.4.1, a):

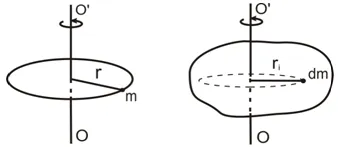
Figura 4.1. Prin definiție a momentului de inerție

În cazul în care un corp solid relativ rotativ la unele arbitrar ales axa OO“, reprezentată sub forma unui sistem și dm momentele de inerție în masă a sumei masei elementare așa-numita, obținem momentul de inerție totală a corpului:

I = Ii = dmiri 2 = r 2 dm,

unde ri - raza de rotație i-lea unitate de masă, iar integrala este preluat întregul volum al corpului (Figura 4.1b.).

Pentru corpurile omogene pentru care densitatea ρ = m / V (unde m - masa corpului, și V - volumul său, adică densitatea se determină masa conținută în unitatea de volum), momentul de inerție se calculează prin formula:

I = ∫r 2 dm = ∫r 2 PDV = p∫r 2 dv, adică I = ρr 2 dV.

Mai jos sunt valorile momentelor de inerție pentru unele corpuri omogene de formă regulată, cu o masă m în raport cu o axă care trece prin centrul de masă al corpului.

Momentele de inerție corpuri de formă corectă