Metoda Chords - informatică, programare
Soluție de ecuații neliniare
Să considerăm ecuația f (x) = 0, unde f (x) - o funcție continuă având un interval (a, b) derivați ai primului și al doilea ordin. Rădăcina este considerat separat și stocat pe intervalul [a, b].
Ideea coardele metodei este că, la un interval suficient de mic [a, b] arc al curbei y = f (x) poate fi înlocuită cu o coardă și o valoare aproximativă a rădăcinii ia punctul de intersecție cu axa abscisă. Să considerăm cazul (Fig. 1), atunci când prima și a doua sunt derivații de același semn, adică f „(x) f ² (x)> 0. Ecuația coardei care trece prin punctele A0 și B, are forma
.
Root aproximare x = x1, pentru care y = 0, este definit ca
.
rădăcină în mod similar, pentru o coardă care trece prin punctele A1 și B, următoarea apropiere se calculează
.
In general, metoda formula coardele are forma:
În cazul în care primul și al doilea derivați au diferite semne, adică,
tot mai aproape de rădăcina x * sunt efectuate de marginea din dreapta a segmentului [a, b], așa cum se arată în Fig. 2, și calculată cu formula:
Selectarea formulei în fiecare caz depinde de forma funcției f (x) și se realizează conform intervalului de delimitare regulă fixă este [a, b] izolație rădăcină, pentru care funcția semnul coincide cu semnul al doilea derivat. Formula (2) este utilizată în cazul în care f (b) f "(b)> 0. Dacă inegalitatea f (a) f" (a)> 0, este necesar să se aplice cu formula (3).



Procesul iterativ continuă până când metoda coardei până când se obține o rădăcină aproximativă cu un grad specificat de precizie. puteți utiliza atunci când se evaluează eroarea raportul de apropiere:
.
Apoi, starea de finalizare de calcul este scris ca:
în cazul în care e - definit erori de calcul. Trebuie remarcat faptul că, în determinarea metodei coardei rădăcină oferă adesea o convergență mai rapidă decât metoda de împărțire în două.
4. Metoda lui Newton (tangențial)
Lăsați ecuația (1) are o rădăcină pe intervalul [a, b], unde f „(x) și f„(x) sunt continue și de semn constant pe tot intervalul [a, b].
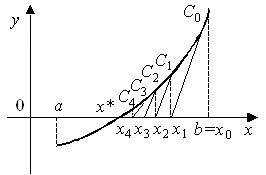
Sensul geometric al metodei lui Newton este că arcul curbei y = f (x) se înlocuiește cu tangenta. În acest scop, selectați o rădăcini inițiale ghici x0 în intervalul [a, b] și are loc la un punct tangent C0 (x0, f (x0)) la curba y = f (x) până la intersecția cu axa x (fig. 3). Ecuația tangentei la punctul C0 ia forma
y = f (x0) + f „(x0) x (x - x0).
Mai mult, pentru abordarea luate x1 abscisă rădăcină, pentru care y = 0:
Apoi, o linie tangentă prin noul punct C1 (x1, f (x1)) și este determinată de punctul de intersecție x2 sale cu axa 0x și etc. În general, formula metodei tangentei are forma:
Rezultatul calculelor este o secvență de valori aproximative x1, x2. xi. fiecare termen de care este mai aproape de rădăcina lui x *, decât cea anterioară. Procesul iterativ se termină de obicei când condiția (4).
X0 inițială armonizare trebuie să îndeplinească condiția:
f (x0) f ¢¢ (x0)> 0. (6)
În caz contrar, convergența metodei Newton nu este garantată, deoarece tangenta intersectează abscisa la un punct nu aparține intervalului [a, b]. În practică, într-o rădăcină inițială aproximare x0, de obicei selectată una dintre limitele intervalului [a, b], adică, x0 = a sau x0 = b, pentru care o marcă funcție coincide cu semnul al doilea derivat.
Metoda lui Newton oferă convergență mare viteză în rezolvarea ecuațiilor pentru care valoarea modulului de ½f derivatului ¢ (x) ½vblizi rădăcină suficient de mare, adică, grafic al funcției y = f (x) are o pantă mai mare în vecinătatea rădăcinii. Dacă curba y = f (x) în intervalul [a, b] este aproape orizontală, metoda tangenta aplicată nu este adecvată.
Un dezavantaj semnificativ al acestei metode este necesitatea de a calcula derivatele organizației pentru procesul iterativ. Dacă valoarea f ¢ (x) se schimbă puțin în intervalul [a, b], este posibil să se simplifice calculele folosind formula
și anume valoarea derivatei suficient pentru a calcula o singură dată la punctul de plecare. Geometric, acest lucru înseamnă că tangentele la punctele Ci (xi, f (xi)), unde i = 1, 2. înlocuite cu linii drepte paralele cu tangenta la curba y = f (x) la punctul C0 inițial (x0, f (x0 )), așa cum se arată în Fig. 4.
În concluzie, trebuie remarcat faptul că toate cele de mai sus deține, în cazul în care x0 inițială ghici este ales suficient de aproape de adevărata rădăcină a ecuației x *. Cu toate acestea, nu este întotdeauna ușor de făcut. Prin urmare, metoda lui Newton este adesea folosit în etapa finală de rezolvare a ecuațiilor după lucrarea unui algoritm convergent fiabil, de exemplu, metoda de împărțire în două.
5. Metoda iteratie simplu
Pentru a aplica această metodă la soluția de (1) pentru a se converti la forma. În continuare, aproximarea inițială este selectată și calculat x1, x2 apoi etc.:
x1 = j (x0); x2 = j (x1); ...; xk = j (xk-1);.
neliniară rădăcină ecuație algebrică
Secvența rezultată este convergent la rădăcina în următoarele condiții:
1) Funcția j (x) este diferențiabilă în intervalul [a, b].
2) la toate punctele j interval ¢ (x) satisface inegalitatea:
0 £ q £ 1. (8)
În aceste condiții rata de convergență este liniară, iar iterație trebuie efectuată până la doar până când devine condiția:
.
,
poate fi utilizat numai pentru 0 £ q £ ½. În caz contrar, iterația se termină prematur, fără a oferi precizia necesară. În cazul în care calculul q este dificil, puteți utiliza criteriul capătului de tip
; .
Diferite metode de conversie ecuațiile (1) la forma. Acesta ar trebui să selecteze una care satisface condiția (8), care generează un proces iterativ convergent, cum se arată în Fig. 5 și 6. În caz contrar, în special atunci când ½j ¢ (x) ½> 1, iterare proces dispersează și nu permite obținerea unei soluții (Fig. 7).



Problema îmbunătățirii calității calcul ecuații neliniare folosind o varietate de metode, cum ar fi o nepotrivire între dorit și real, vor exista în viitor. Această decizie va contribui la dezvoltarea tehnologiei informației, care constă în îmbunătățirea metodelor de organizare a proceselor de informare și punerea în aplicare a acestora prin intermediul unor instrumente specifice - limbaje de programare și medii.
bibliografie
2. Abramov SA iarna EV - Începe programare în Pascal. - M. Science, 1987. -112 p.
Soluție de ecuații neliniare
Informații despre „Soluția de ecuații neliniare“