Listă ( „masă“) integralele de bază

Enumerăm integralelor funcțiilor elementare, care sunt numite uneori tabel:

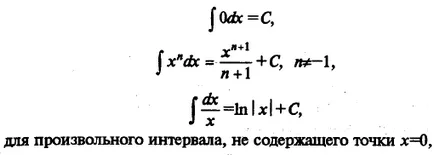
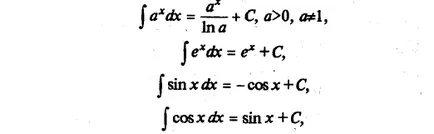
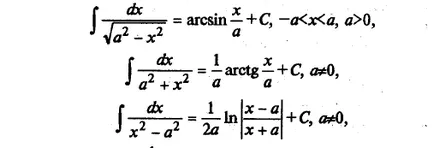
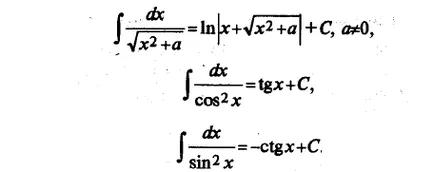
Oricare dintre formulele de mai sus poate fi demonstrată prin luarea derivata partea dreaptă (ca rezultat al funcției integrandul este obținută).

metode de integrare

Să luăm în considerare câteva dintre metodele de bază ale integrării. Printre acestea se numără:

1. Metoda de descompunere (integrare directă).

Această metodă se bazează pe utilizarea directă a integralelor tabulare, precum și aplicarea proprietăților 4 și 5 ale nedefinită integralei (adică la îndepărtarea parantezele factorul constant și / sau prezentarea integrantul ca sumă a funcțiilor - descompunerea integrantul în termeni).

Exemplul 1. De exemplu, pentru nahozhdeniya (dx / x 4), se poate folosi direct tabular dlyax integral n dx. De fapt,  (dx / x 4) = x -4 dx = x -3 / (- 3) + C = -1 / 3x 3 + C.

Luați în considerare câteva exemple.

Exemplul 2. La aceeași nahozhdeniyavospolzuemsya integrală:

Exemplul 3. Pentru a lua nahozhdeniyanado

Exemplul 4: Pentru a găsi, reprezentăm integrandul în videi utilizare tabelară integrală pentru funcția exponențială:

Luați în considerare utilizarea eliminarea factorului permanent între paranteze.

exemplu EXEMPLUL 5.Naydem. Având în vedere că. obținem

EXEMPLUL 6 Să ne. Din moment ce folosim integralomPoluchim tabular

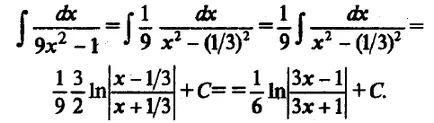
Următoarele două exemple pot fi de asemenea folosite pentru îndepărtarea capselor și integralele tabelate:

Să luăm în considerare mai multe exemple complexe, în care integrantă a sumei utilizate.

Exemplul 9. De exemplu, găsim

. Pentru a aplica metoda de descompunere în numărătorul formulei pentru cantitatea de utilizare a  cub. iar apoi polinomul rezultat este împărțit prin termenul numitorul prin termenul.

=  ((8x 3/2 + 12x + 6x 1/2 + 1) / (x 3/2)) dx =  (8 + 12x + -1/2 6 / x + x -3/2) dx = 8 dx + 12x -1/2 dx + + 6dx / x + x -3/2 dx =

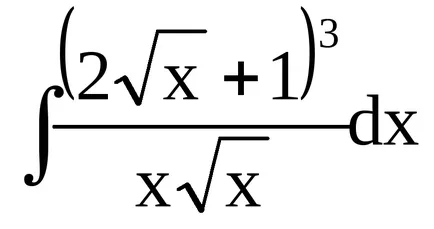
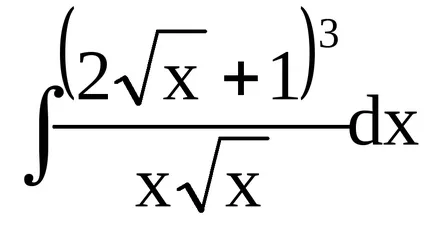
Trebuie remarcat faptul că la sfârșitul soluții complete înregistrate generale constante C (nu individuale prin integrarea fiecare termen). În viitor, de asemenea, oferit să omită procesul de integrare a soluțiilor permanente termenii individuali, atâta timp cât expresia conține cel puțin o nedefinită integrală (vom scrie o soluție permanentă în final).

10. EXEMPLUL Să ne. Pentru a rezolva această problemă la factorul numarator (apoi să fie capabil de a reduce numitor).

11. EXEMPLUL Să. Puteți folosi identități trigonometrice.

Uneori, în scopul de a descompune expresia în termeni, este necesar să se utilizeze tehnici mai sofisticate.

12. EXEMPLU Să ne. În integrandul vom selecta partea întreagă a fracțiunii. atunci

.

13. EXEMPLUL Să ne

2. Metoda variabilă de înlocuire (metoda de substituție)

Metoda se bazează pe următoarea formulă: f (x) dx = f ( (t)) ` (t) dt, unde x =  (t) - o funcție care este diferențiabilă în intervalul considerat.

Dovada. Am găsit derivați variabilă TGI din stânga și din dreapta ale formulei.

Rețineți că partea stângă este o funcție complicată, care este un argument intermediar x =  (t). Prin urmare, să se diferențieze de t, este primul integral diferențiabilă peste x, atunci derivatul vozmem argumentației respect intermediar la t.

Derivatul din partea dreaptă:

Deoarece acești derivați sunt, pentru investigarea teorema lui Lagrange stânga și dreapta au dovedit formule diferă printr-o constantă. Deoarece integralelor nedefinite înșiși sunt definite până la un termen constant nedeterminat, constanta specificată poate fi coborâtă în înregistrarea finală. Sa dovedit.

schimbarea cu succes a variabilelor pentru a simplifica integralei originale, iar în cazurile cele mai simple, să-l reducă la masa. La aplicarea acestei metode disting metode de substituție liniare și neliniare.

a) metoda de substituție liniară de exemplu.

Exemplul 1.

. Pustt = 1 - 2x, atunci

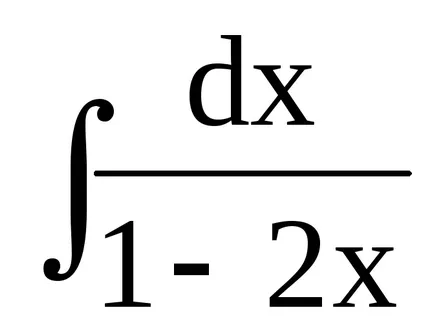
Trebuie remarcat faptul că o nouă variabilă, nu se poate scrie în mod clar. În astfel de cazuri, se spune despre funcția de conversie a unei mărci diferențiale sau introducerea unei mărci diferențiale fixe și variabile - adică modificarea implicită a variabilei.

Exemplul 2. De exemplu, naydemcos (3x + 2) dx. Prin proprietăți diferențiale dx = (1/3) d (3x) = (1/3) d (3x + 2), togdacos (3x + 2) dx =  (1/3) cos (3x + 2) d (3x + + 2) = (1/3) cos (3x + 2) d (3x + 2) = (1/3) sin (3x + 2) + C.

In ambele aceste exemple a fost utilizat permutare t liniar = kx + b (k0) pentru a găsi integralele.

În general, următoarea teoremă deține.

Teorema despre substituție liniară. Fie F (x) - un primitiv pentru funcția f (x). Togdaf (kx + b) dx = (1 / k) F (kx + b) + C, unde k și b - sunt constante, k0.

Prin definiție f integrală (kx + b) d (kx + b) = F (kx + b) + C. Hod (kx + b) = (kx + b) `dx = kdx. Rendered mnozhitelkza constant semn integral: kf (kx + b) dx = F (kx + b) + C. Acum este posibil să se împartă în partea stângă și dreaptă a ecuației pentru a obține Naki afirmație corectă pentru a se referi la un termen constant.

Această teoremă afirmă că, dacă definiția f integral (x) dx = F (x) + C, în locul expresiei argument x înlocuitor (kx + b), aceasta va conduce la un factor suplimentar de 1 / kpered primitiv.

Următoarele exemple vor rezolva Folosind teorema de mai sus.

S-au găsit. Zdeskx + b = 3 -x, t.e.k = -1, b = 3. Apoi

S-au găsit. Zdeskx + b = 4x + 3, t.e.k = 4, b = 3. Apoi

S-au găsit. Zdeskx + b = -2x + 7 t.e.k = -2, b = 7. Apoi

.

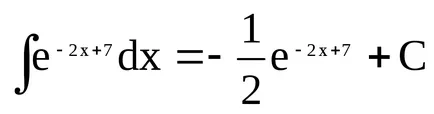
EXEMPLUL 6 Să ne

. Zdeskx + b = 2x + 0 t.e.k = 2, b = 0.

.

Comparați acest rezultat cu exemplul 8, care a fost rezolvată prin descompunere. Rezolvarea acestei probleme este o altă metodă, am primit răspunsul

. Comparam rezultatele:. Astfel, aceste expresii difera printr-un termen constant, și anume răspunsurile nu intră în conflict unele cu altele.

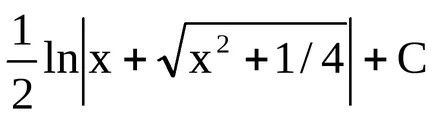
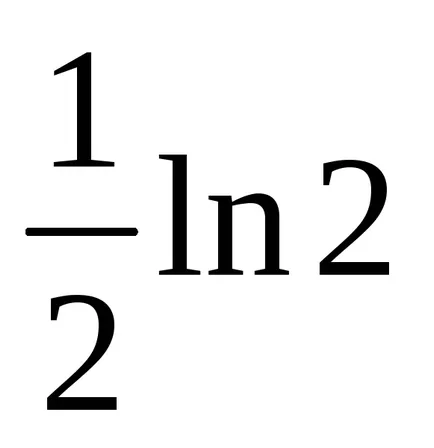
Exemplul 7. Găsim

. Distingem în numitorul unui pătrat perfect.

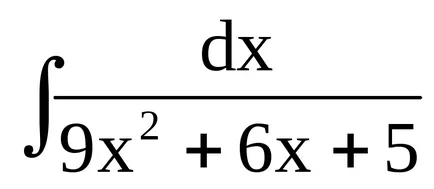
În unele cazuri, înlocuirea variabilei nu reduce integralei direct la masa, dar se poate simplifica soluția, făcând posibilă utilizarea într-o etapă ulterioară a metodei de descompunere.

Exemplul 8 De exemplu, găsiți. Zamenimt = x + 2, togdadt = d (x + 2) = dx. atunci

,

unde C = C1 - 6 (dacă este substituit în vmestotvyrazheniya (x + 2) în loc de primii doi termeni ½x obține 2 -2x- 6).

Exemplul 9. Să

. Pustt = 2x + 1, togdadt = 2DX; dx = ½dt; x = (t- 1) / 2.

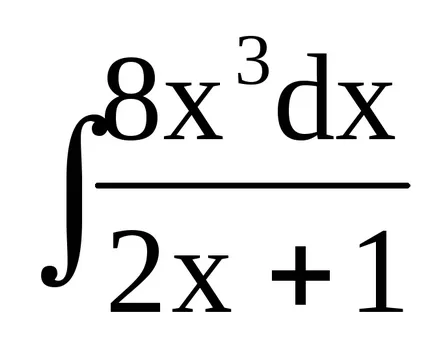
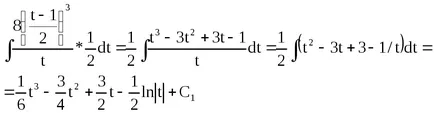
Înlocuim tvyrazhenie (2x + 1), și dezvăluie paranteze dau altele asemenea.

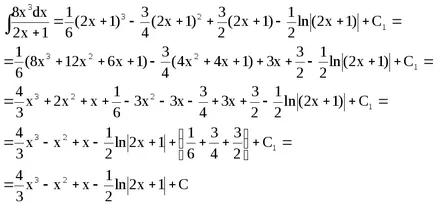
Rețineți că, în procesul de schimbare, ne-am mutat într-un termen constant diferit, din moment ce Grupa termeni constante în procesul de transformare poate fi omisă.

b) o metodă de substituție neliniară, luați în considerare exemplul următor.

Exemplul 1.

. Pustt = -x 2. Apoi poate fi exprimată x cherezt, apoi găsi o expresie pentru DXI realiza schimbarea variabilei în integralei dorită. Dar, în acest caz, este mai ușor de a face altfel. Naydemdt = d (-x 2) = -2xdx. Rețineți că vyrazheniexdxyavlyaetsya un factor de integrandul în această integrală. O exprimăm din ravenstvaxdx rezultată = - ½dt. atunci

=  (- ½) e t dt = (- ½)  e t dt = (- ½) e t + C = (- ½)+ C

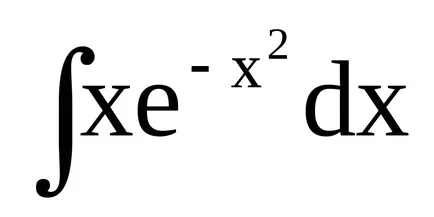
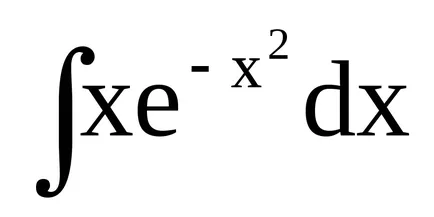
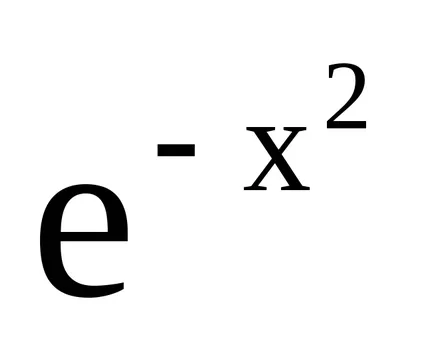
Luați în considerare câteva exemple.

Exemplul 2. Găsiți. Pustt = 1 -x 2. Apoi

;

Exemplul 3 Să. = Pustt. atunci

;

Exemplul 4. În cazul substituției nelineară, de asemenea, este convenabil să se utilizeze o modificare implicită a variabilei.

De exemplu, vom găsi

. Zapishemxdx = = (-1/4) d (3 - 2x 2) (implicit înlocuit peremennoyt = 3 - 2x 2). atunci

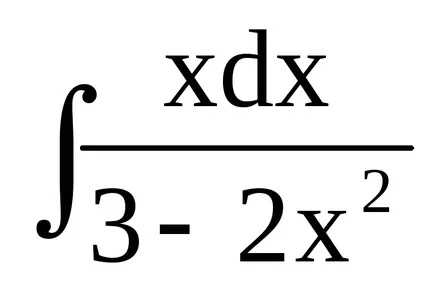
EXEMPLUL 5 Să ne. Aici, de asemenea, introducem o marcă diferențială variabilă (implicit zamenat 3 + 5x = 3). atunci

EXEMPLUL 6 Să ne. deoarece,

.

Exemplul 7. Să ne. de atunci

Luați în considerare câteva exemple în care există necesitatea de a combina substituția diferite.

Exemplul 8. a găsit. Pustt = 2x + 1, togdax = (t- 1) / 2; dx = ½dt.

Exemplul 9. a găsit. Pustt = x- 2 togdax = t + 2; dx = dt.